AIXI

AIXI ['ai̯k͡siː] is a mathematical formalism for artificial general intelligence. It combines Solomonoff induction with sequential decision theory. AIXI was first proposed by Marcus Hutter in 2000^[1] and the results below are proved in Hutter's 2005 book Universal Artificial Intelligence.^[2]

AIXI is a reinforcement learning agent; it maximizes the expected total rewards received from the environment. Intuitively, it simultaneously considers every computable hypothesis. In each time step, it looks at every possible program and evaluates how many rewards that program generates depending on the next action taken. The promised rewards are then weighted by the subjective belief that this program constitutes the true environment. This belief is computed from the length of the program: longer programs are considered less likely, in line with Occam's razor. AIXI then selects the action that has the highest expected total reward in the weighted sum of all these programs.

Definition

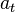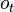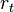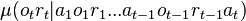The AIXI agent interacts sequentially with some (stochastic and unknown to AIXI) environment $\mu$ . In step t, the agent outputs an action $a_t$ and the environment responds with an observation $o_t$ and a reward $r_t$ distributed according to the conditional probability $\mu(o_t r_t | a_1 o_1 r_1 ... a_{t-1} o_{t-1} r_{t-1} a_t)$ . Then this cycle repeats for t + 1. 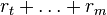The agent tries to maximize cumulative future reward $r_t + \ldots + r_m$ for a fixed lifetime m.

Given a current time t and history 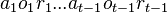$a_1 o_1 r_1 ... a_{t-1} o_{t-1} r_{t-1}$ , the action AIXI outputs is defined as^[3]

\arg \max_{a_t} \sum_{o_t r_t} \ldots \max_{a_m} \sum_{o_m r_m} [r_t + \ldots + r_m] \sum_{q:\; U(q, a_1 \ldots a_m) = o_1 r_1 \ldots o_m r_m} 2^{-\textrm{length}(q)},

where U denotes a monotone universal Turing machine, and q ranges over all programs on the universal machine U.

The parameters to AIXI are the universal Turing machine and the agent's lifetime m. The latter dependence can be removed by the use of discounting.

Optimality

AIXI's performance is measured by the expected total number of rewards it receives. AIXI has been proven to be optimal in the following ways.^[2]

Pareto optimality: there is no other agent that performs at least as well as AIXI in all environments while performing strictly better in at least one environment.
Balanced Pareto optimality: Like Pareto optimality, but considering a weighted sum of environments.
Self-optimizing: a policy p is called self-optimizing for an environment $\mu$ if the performance of p approaches the theoretical maximum for $\mu$ when the length of the agent's lifetime (not time) goes to infinity. For environment classes where self-optimizing policies exist, AIXI is self-optimizing.

Computational aspects

Like Solomonoff induction, AIXI is incomputable. However, there are computable approximations of it. One such approximation is AIXItl, which performs as least as well as the provably best time t and space l limited agent.^[2] Another approximation to AIXI with a restricted environment class is MC-AIXI(FAC-CTW), which has had some success playing simple games such as partially observable Pac-Man.^[4]^[5]

References

↑ Marcus Hutter (2000). A Theory of Universal Artificial Intelligence based on Algorithmic Complexity. arXiv:cs.AI/0004001.
↑ 2.0 2.1 2.2 — (2004). Universal Artificial Intelligence: Sequential Decisions Based on Algorithmic Probability. Springer. doi:10.1007/b138233. ISBN 978-3-540-22139-5.
↑ http://hutter1.net/ai/uaibook.htm
↑ Veness, Joel; Kee Siong Ng; Hutter, Marcus; Uther, William; Silver, David (2009). "A Monte Carlo AIXI Approximation". arXiv:0909.0801 [cs.AI].
↑ http://www.youtube.com/watch?v=yfsMHtmGDKE