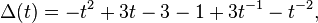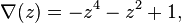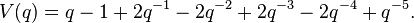6₂ knot

6₂ knot
Arf invariant 1
Braid length 6
Braid no. 3
Bridge no. 2
Crosscap no. 2
Crossing no. 6
Genus 2
Hyperbolic volume 4.40083
Stick no. 8
Unknotting no. 1
Conway notation [312]
A-B notation 62
Dowker notation 4, 8, 10, 12, 2, 6
Last /Next 61 / 63
Other
alternating, hyperbolic, fibered, prime, reversible, twist

In knot theory, the 62 knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 63 knot. This knot is sometimes referred to as the Miller Institute knot,[1] because it appears in the logo[2] of the Miller Institute for Basic Research in Science at the University of California, Berkeley.

The 62 knot is invertible but not amphichiral. Its Alexander polynomial is

\Delta(t) = -t^2 + 3t - 3 - 1 + 3t^{-1} - t^{-2}, \,

its Conway polynomial is

\nabla(z) = -z^4 - z^2 + 1, \,

and its Jones polynomial is

V(q) = q - 1 + 2q^{-1} - 2q^{-2} + 2q^{-3} - 2q^{-4} + q^{-5}. \, [3]

The 62 knot is a hyperbolic knot, with its complement having a volume of approximately 4.40083.

References

  1. ↑ Weisstein, Eric W., "Miller Institute Knot", MathWorld.
  2. ↑ Miller Institute - Home Page
  3. ↑ "6_2", The Knot Atlas.