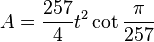257-gon

Regular 257-gon

A regular 257-gon
Type Regular polygon
Edges and vertices 257
Schläfli symbol {257}
Coxeter diagram
Symmetry group Dihedral (D257), order 2×257
Internal angle (degrees) ≈178.60°
Dual polygon self
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non-self-intersecting 257-gon is 91800°.

The area of a regular 257-gon is (with t = edge length)

A = \frac{257}{4} t^2 \cot \frac{\pi}{257}

A whole regular 257-gon is not visually discernible from a circle, and its perimeter differs from that of the circumscribed circle by about 24 parts per million.

Regular 257-gon construction

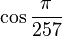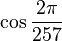The regular 257-gon (one with all sides equal and all angles equal) is of interest for being a constructible polygon: that is, it can be constructed using a compass and an unmarked straightedge. This is because 257 is a Fermat prime, being of the form 22n + 1 (in this case n = 3). Thus, the values \cos \frac{\pi}{257} and \cos \frac{2\pi}{257} are 128-degree algebraic numbers, and like all constructible numbers they can be written using square roots and no higher-order roots.

Although it was known to Gauss by 1801 that the regular 257-gon was constructible, the first explicit constructions of a regular 257-gon were given by Magnus Georg Paucker (1822)[1] and Friedrich Julius Richelot (1832).[2] Another method involves the use of 150 circles, 24 being Carlyle circles: this method is pictured below. One of these Carlyle circles solves the quadratic equation x2 + x − 64 = 0.[3]

257-gram

A 257-gram is a 257-sided star polygon. As 257 is prime, there are 127 regular forms generated by Schläfli symbols {257/n} for all integers 2 ≤ n ≤ 128 as 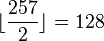\lfloor \frac{257}{2} \rfloor = 128.

Below is a view of {257/128}, with 257 nearly radial edges, with its star vertex internal angles 360/257° (~0.7°).[4]

References

  1. ↑ Magnus Georg Paucker (1822). "Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundersiebenundfünfzig-Ecks in den Kreis". Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst (in German) 2: 160–219.
  2. ↑ Friedrich Julius Richelot (1832). "De resolutione algebraica aequationis x257 = 1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata". Journal für die reine und angewandte Mathematik (in Latin) 9: 1–26, 146–161, 209–230, 337–358. doi:10.1515/crll.1832.9.337.
  3. ↑ DeTemple, Duane W. (Feb 1991). "Carlyle circles and Lemoine simplicity of polygon constructions". The American Mathematical Monthly 98 (2): 97–208. doi:10.2307/2323939. Retrieved 6 November 2011.
  4. ↑ 0.700389=180(1-2/(257/128))=180(1-256/257)=180/257=360/257