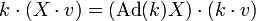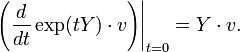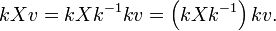(g,K)-module
In mathematics, more specifically in the representation theory of reductive Lie groups, a 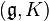 -module is an algebraic object, first introduced by Harish-Chandra,[1] used to deal with continuous infinite-dimensional representations using algebraic techniques. Harish-Chandra showed that the study of irreducible unitary representations of a real reductive Lie group, G, could be reduced to the study of irreducible
-module is an algebraic object, first introduced by Harish-Chandra,[1] used to deal with continuous infinite-dimensional representations using algebraic techniques. Harish-Chandra showed that the study of irreducible unitary representations of a real reductive Lie group, G, could be reduced to the study of irreducible 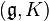 -modules, where
-modules, where  is the Lie algebra of G and K is a maximal compact subgroup of G.[2]
is the Lie algebra of G and K is a maximal compact subgroup of G.[2]
Definition
Let G be a real Lie group. Let  be its Lie algebra, and K a maximal compact subgroup with Lie algebra
be its Lie algebra, and K a maximal compact subgroup with Lie algebra 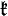 . A
. A  -module is defined as follows:[3] it is a vector space V that is both a Lie algebra representation of
-module is defined as follows:[3] it is a vector space V that is both a Lie algebra representation of  and a group representation of K (without regard to the topology of K) satisfying the following three conditions
and a group representation of K (without regard to the topology of K) satisfying the following three conditions
- 1. for any v ∈ V, k ∈ K, and X ∈

- 2. for any v ∈ V, Kv spans a finite-dimensional subspace of V on which the action of K is continuous
- 3. for any v ∈ V and Y ∈
In the above, the dot,  , denotes both the action of
, denotes both the action of  on V and that of K. The notation Ad(k) denotes the adjoint action of G on
on V and that of K. The notation Ad(k) denotes the adjoint action of G on  , and Kv is the set of vectors
, and Kv is the set of vectors 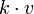 as k varies over all of K.
as k varies over all of K.
The first condition can be understood as follows: if G is the general linear group GL(n, R), then  is the algebra of all n by n matrices, and the adjoint action of k on X is kXk−1; condition 1 can then be read as
is the algebra of all n by n matrices, and the adjoint action of k on X is kXk−1; condition 1 can then be read as
In other words, it is a compatibility requirement among the actions of K on V,  on V, and K on
on V, and K on  . The third condition is also a compatibility condition, this time between the action of
. The third condition is also a compatibility condition, this time between the action of 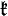 on V viewed as a sub-Lie algebra of
on V viewed as a sub-Lie algebra of  and its action viewed as the differential of the action of K on V.
and its action viewed as the differential of the action of K on V.
Notes
- ↑ Page 73 of Wallach 1988
- ↑ Page 12 of Doran & Varadarajan 2000
- ↑ This is James Lepowsky's more general definition, as given in section 3.3.1 of Wallach 1988
References
- Doran, Robert S.; Varadarajan, V. S., eds. (2000), The mathematical legacy of Harish-Chandra, Proceedings of Symposia in Pure Mathematics 68, AMS, ISBN 978-0-8218-1197-9, MR 1767886
- Wallach, Nolan R. (1988), Real reductive groups I, Pure and Applied Mathematics 132, Academic Press, ISBN 978-0-12-732960-4, MR 0929683