(a,b)-decomposability
In graph theory, the (a, b)-decomposability of an undirected graph is the existence of a partition of its edges into a + 1 sets, each one of them inducing a forest, except one who induces a graph with maximum degree b. If this graph is also a forest, then we call this a F(a, b)-decomposition.
A graph with arboricity a is (a, 0)-decomposable. Every (a, 0)-decomposition or (a, 1)-decomposition is a F(a, 0)-decomposition or a F(a, 1)-decomposition respectively.
Graph Classes
- Every planar graph is F(2,4)-decomposable.[1]
- Every planar graph
 with girth at least
with girth at least 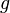 is
is
- Every outerplanar graph is F(2,0)-decomposable[2] and (1,3)-decomposable.[8]
Notes
- ↑ Gonçalves (2009), conjectured by Balogh et al. (2005). Improving results by Nash-Williams (1964) then Balogh et al. (2005).
- ↑ 2.0 2.1 Implied by Nash-Williams (1964).
- ↑ He et al. (2002)
- ↑ Implied by Montassier et al. (2012), improving results by He et al. (2002), then Kleitman (2008).
- ↑ Independently proved by Yang & Zhang (2011) and implied by Montassier et al. (2012), improving results by He et al. (2002) for girth 11, then Bassa et al. (2010) for girth 10 and Borodin et al. (2008a) for girth 9.
- ↑ Borodin et al. (2009b), even if not explicitly stated.
- ↑ Borodin et al. (2009a), improving results by He et al. (2002), then Borodin et al. (2008b).
- ↑ Proved without explicit reference by Guan & Zhu (1999).
References (chronological order)
- Nash-Williams, Crispin St. John Alvah (1964). "Decomposition of finite graphs into forests". Journal of the London Mathematical Society 39 (1): 12. doi:10.1112/jlms/s1-39.1.12. MR 0161333.
- Guan, D. J.; Zhu, Xuding (1999). "Game chromatic number of outerplanar graphs". Journal of Graph Theory 30 (1): pp. 67–70. doi:10.1002/(sici)1097-0118(199901)30:1<67::aid-jgt7>3.0.co;2-m.
- He, Wenjie; Hou, Xiaoling; Lih, Ko-Wei; Shao, Jiating; Wang, Weifan; Zhu, Xuding (2002). "Edge-partitions of planar graphs and their game coloring numbers". Journal of Graph Theory 41: pp. 307–311. doi:10.1002/jgt.10069.
- Balogh, József; Kochol, Martin; Pluhár, András; Yu, Xingxing (2005). "Covering planar graphs with forests". Journal of Combinatorial Theory, Series B 94 (1): pp. 147–158. doi:10.1016/j.ejc.2007.06.020.
- Borodin, Oleg V.; Kostochka, Alexandr V.; Sheikh, Naeem N.; Yu, Gexin (2008). "Decomposing a planar graph with girth 9 into a forest and a matching". European Journal of Combinatorics 29 (5): pp. 1235–1241. doi:10.1016/j.ejc.2007.06.020.
- Borodin, Oleg V.; Kostochka, Alexandr V.; Sheikh, Naeem N.; Yu, Gexin (2008). "M-Degrees of Quadrangle-Free Planar Graphs". Journal of Graph Theory 60 (1): pp. 80–85. doi:10.1002/jgt.20346.
- Kleitman, Daniel J. (2008). "Partitioning the Edges of a Girth 6 Planar Graph into those of a Forest and those of a Set of Disjoint Paths and Cycles". Manuscript.
- Gonçalves, Daniel (2009). "Covering planar graphs with forests, one having bounded maximum degree". Journal of Combinatorial Theory, Series B 99 (2): pp. 314–322. doi:10.1016/j.jctb.2008.07.004.
- Borodin, Oleg V.; Ivanova, Anna O.; Kostochka, Alexandr V.; Sheikh, Naeem N. (2009). "Decompositions of Quadrangle-Free Planar Graphs". Discussiones Mathematicae Graph Theory 29: pp. 87–99. doi:10.7151/dmgt.1434.
- Borodin, Oleg V.; Ivanova, Anna O.; Kostochka, Alexandr V.; Sheikh, Naeem N. (2009). "Planar graphs decomposable into a forest and a matching". Discrete Mathematics 309 (1): pp. 277–279. doi:10.1016/j.disc.2007.12.104.
- Bassa, A.; Burns, J.; Campbell, J.; Deshpande, A.; Farley, J.; Halsey, L.; Ho, S.-Y.; Kleitman, D.; Michalakis, S.; Persson, P.-O.; Pylyavskyy, P.; Rademacher, L.; Riehl, A.; Rios, M.; Samuel, J.; Tenner, B.E.; Vijayasarathy, A.; Zhao, L. (2010). "Partitioning a Planar Graph of Girth 10 into a Forest and a Matching". European Journal of Combinatorics 124 (3): pp. 213–228. doi:10.1111/j.1467-9590.2009.00468.x.
- Wang, Yingqian; Zhang, Qijun (2011). "Decomposing a planar graph with girth at least 8 into a forest and a matching". Discrete Mathematics 311 (10-11): pp. 844–849. doi:10.1016/j.disc.2011.01.019.
- Montassier, Mickaël; Ossona de Mendez, Patrice; André, Raspaud; Zhu, Xuding (2012). "Decomposing a graph into forests". Journal of Combinatorial Theory, Series B 102 (1): pp. 38–52. doi:10.1016/j.jctb.2011.04.001.
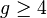 .
.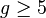 .
.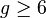 .
.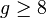 ,
,