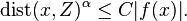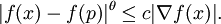Łojasiewicz inequality

In real algebraic geometry, the Łojasiewicz inequality, named after Stanisław Łojasiewicz, gives an upper bound for the distance of a point to the nearest zero of a given real analytic function. Specifically, let ƒ : U → R be a real-analytic function on an open set U in Rn, and let Z be the zero locus of ƒ. Assume that Z is not empty. Then for any compact set K in U, there exist positive constants α and C such that, for all x in K

\operatorname{dist}(x,Z)^\alpha \le C|f(x)|. \,

Here α can be large.

The following form of this inequality is often seen in more analytic contexts: with the same assumptions on ƒ, for every p ∈ U there is a possibly smaller open neighborhood W of p and constants θ ∈ (0,1) and c > 0 such that

|f(x)-f(p)|^\theta\le c|\nabla f(x)|. \,

References