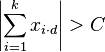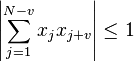±1-sequence

In mathematics, a ±1–sequence is a sequence of numbers, each of which is either 1 or −1. One example is the sequence $(x 1, x 2, x 3, ...)$ , where $x i = (- 1) i +1$ .

Such sequences are commonly studied in discrepancy theory.

Erdős discrepancy problem

Around 1932 mathematician Paul Erdős conjectured that for any infinite ±1-sequence 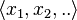$\textstyle\langle x_1, x_2, ..\rangle$ and any integer C, there exist integers k and d such that:

\left| \sum_{i=1}^k x_{i\cdot d} \right| > C

The Erdős Discrepancy Problem asks for a proof or disproof of this conjecture.

In October 2010, this problem was taken up by the Polymath Project.^[1]

In February 2014, Alexei Lisitsa and Boris Konev of the University of Liverpool, UK, ^[2] showed that every sequence of 1161 or more elements satisfies the conjecture in the special case C = 2, which proves the conjecture for C ≤ 2. As of February 2014, this is the best such bound available. Their proof relies on a SAT-solver computer algorithm whose output takes up 13 gigabytes of data, more than the entire text of Wikipedia, so it cannot be verified by human mathematicians. However, human checking may not be necessary: if an independent computer verification returns the same results, the proof is likely to be correct.^[3]

Barker codes

Main article: Barker code

A Barker code is a sequence of N values of +1 and −1,

x_j

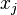for j = 1, 2, …, N

such that

\left|\sum_{j=1}^{N-v} x_j x_{j+v}\right| \le 1\,

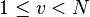for all $1 \le v < N$ .^[4]

Barker codes of length 11 and 13 are used in direct-sequence spread spectrum and pulse compression radar systems because of their low autocorrelation properties.

Notes

↑ "The Erdős discrepancy problem". Polymath Project.
↑ Konev, Boris; Lisitsa, Alexei (17 Feb 2014). "A SAT Attack on the Erdos Discrepancy Conjecture". arXiv:1402.2184.
↑ Aron, Jacob (February 17, 2014). "Wikipedia-size maths proof too big for humans to check". New Scientist. Retrieved February 18, 2014.
↑ Barker, R. H. (1953). "Group Synchronizing of Binary Digital Sequences". Communication Theory. London: Butterworth. pp. 273–287.

References

Chazelle, Bernard. The Discrepancy Method: Randomness and Complexity. Cambridge University Press. ISBN 0-521-77093-9.

External links