Zonal polynomial

From Wikipedia, the free encyclopedia

In mathematics, a zonal polynomial is a multivariate symmetric homogeneous polynomial. The zonal polynomials form a basis of the space of symmetric polynomials.

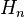They appear as zonal spherical functions of the Gelfand pairs $(S_{{2n}},H_{n})$ (here, $H_{n}$ is the hyperoctahedral group) and 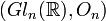$(Gl_{n}({\mathbb {R}}),O_{n})$ , which means that they describe canonical basis of the double class algebras ${\mathbb {C}}[H_{n}\backslash S_{{2n}}/H_{n}]$ and ${\mathbb {C}}[O_{d}({\mathbb {R}})\backslash M_{d}({\mathbb {R}})/O_{d}({\mathbb {R}})]$ .

They are applied in multivariate statistics.

The zonal polynomials are the 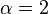$\alpha =2$ case of the C normalization of the Jack function.

References

Robb Muirhead, Aspects of Multivariate Statistical Theory, John Wiley & Sons, Inc., New York, 1984.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.