Zoltán Füredi

From Wikipedia, the free encyclopedia

Zoltán Füredi (Budapest, Hungary, 21 May 1954) is a Hungarian mathematician, working in combinatorics, mainly in discrete geometry and extremal combinatorics. He was a student of Gyula O. H. Katona. He is a corresponding member of the Hungarian Academy of Sciences (2004). He is a research professor of the Rényi Mathematical Institute of the Hungarian Academy of Sciences, and a professor at the University of Illinois Urbana-Champaign (UIUC).

Füredi received his Candidate of Sciences degree in mathematics in 1981 from the Hungarian Academy of Sciences.^[1]

Some results

In infinitely many cases he determined the maximum number of edges in a graph with no C₄.
With Paul Erdős he proved that for some c>1, there are c^d points in d-dimensional space such that all triangles formed from those points are acute.
With Imre Bárány he proved that no polynomial time algorithm determines the volume of convex bodies in dimension d within a multiplicative error d^d.
He proved that there are at most 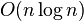$O(n\log n)$ unit distances in a convex n-gon.^[2]
In a paper written with coauthors he solved the Hungarian lottery problem.^[3]
With I. Palásti he found the best known lower bounds on the orchard-planting problem of finding sets of points with many 3-point lines.^[4]

↑ Zoltán Füredi at the Mathematics Genealogy Project
↑ Z. Füredi (1990). "The maximum number of unit distances in a convex n-gon". Journal of Combinatorial Theory 55 (2): 316–320. doi:10.1016/0097-3165(90)90074-7.
↑ Z. Füredi, G. J. Székely, and Z. Zubor (1996). "On the lottery problem". Journal of Combinatorial Designs (Wiley) 4 (1): 5–10. Reprint
↑ Füredi, Z.; Palásti, I. (1984), "Arrangements of lines with a large number of triangles", Proceedings of the American Mathematical Society 92 (4): 561–566 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.