Zero morphism

In category theory, a branch of mathematics, a zero morphism is a special kind of morphism exhibiting properties like the morphisms to and from a zero object.

Definitions

Suppose C is a category, and f : X → Y is a morphism in C. The morphism f is called a constant morphism (or sometimes left zero morphism) if for any object W in C and any g, h : W → X, fg = fh. Dually, f is called a coconstant morphism (or sometimes right zero morphism) if for any object Z in C and any g, h ∈ Mor_C(Y, Z), gf = hf. A zero morphism is one that is both a constant morphism and a coconstant morphism.

A category with zero morphisms is one where, for every two objects A and B in C, there is a fixed morphism 0_AB : A → B such that for all objects X, Y, Z in C and all morphisms f : Y → Z, g : X → Y, the following diagram commutes:

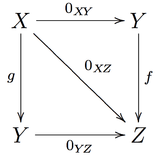
The morphisms 0_XY necessarily are zero morphisms and form a compatible system of zero morphisms.

If C is a category with zero morphisms, then the collection of 0_XY is unique.

This way of defining a "zero morphism" and the phrase "a category with zero morphisms" separately is unfortunate, but if each homset has a ″zero morphism", then the category "has zero morphisms".

Examples

• In the category of groups (or of modules), a zero morphism is a homomorphism f : G → H that maps all of G to the identity element of H. The null object in the category of groups is the trivial group 1 = {1}, which is unique up to isomorphism. Every zero morphism can be factored through 1, i. e., f : G → 1 → H.

• More generally, suppose C is any category with a zero object 0. Then for all objects X and Y there is a unique sequence of morphisms

0_XY : X → 0 → Y

The family of all morphisms so constructed endows C with the structure of a category with zero morphisms.

• If C is a preadditive category, then every morphism set Mor(X,Y) is an abelian group and therefore has a zero element. These zero elements form a compatible family of zero morphisms for C making it into a category with zero morphisms.

• The category Set (sets with functions as morphisms) does not have a zero object, but it does have an initial object, the empty set ∅. The only right zero morphisms in Set are the functions ∅ → X for a set X.

Related concepts

If C has a zero object 0, given two objects X and Y in C, there are canonical morphisms f : 0 → X and g : Y → 0. Then, fg is a zero morphism in Mor_C(Y, X). Thus, every category with a zero object is a category with zero morphisms given by the composition 0_XY : X → 0 → Y.

If a category has zero morphisms, then one can define the notions of kernel and cokernel for any morphism in that category.

References

• Section 1.7 of Pareigis, Bodo (1970), Categories and functors, Pure and applied mathematics 39, Academic Press, ISBN 978-0-12-545150-5 
• Herrlich, Horst; Strecker, George E. (1973), Category Theory, Allen and Bacon, Inc. Boston .