Zariski's lemma
In algebra, Zariski's lemma, introduced by Oscar Zariski, states that if K is a finitely generated algebra over a field k and if K is a field, then K is a finite field extension of k.
An important application of the lemma is a proof of the weak form of Hilbert's nullstellensatz:[1] if I is a proper ideal of ![k[t_{1},...,t_{n}]](/2014-wikipedia_en_all_02_2014/I/media/4/2/1/b/421bfc5463a36d7e8c3e592614c4ed62.png) (k algebraically closed field), then I has a zero; i.e., there is a point x in
(k algebraically closed field), then I has a zero; i.e., there is a point x in 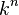 such that
such that 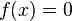 for all f in I.[2]
for all f in I.[2]
The lemma may also be understood from the following perspective. In general, a ring R is a Jacobson ring if and only if every finitely generated R-algebra that is a field is finite over R.[3] Thus, the lemma follows from the fact that a field is a Jacobson ring.
Proof
Two direct proofs, one of which is due to Zariski, are given in Atiyah–MacDonald.[4][5] The lemma is also a consequence of the Noether normalization lemma. Indeed, by the normalization lemma, K is a finite module over the polynomial ring ![k[x_{1},\ldots ,x_{d}]](/2014-wikipedia_en_all_02_2014/I/media/e/a/0/4/ea042c2dee263df9ca98af96545226f4.png) where
where  are algebraically independent over k. But since K has Krull dimension zero, the polynomial ring must have dimension zero; i.e.,
are algebraically independent over k. But since K has Krull dimension zero, the polynomial ring must have dimension zero; i.e., 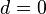 .
.
In fact, the lemma is a special case of the general formula 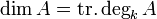 for a finitely generated k-algebra A that is an integral domain, which is also a consequence of the normalization lemma.
for a finitely generated k-algebra A that is an integral domain, which is also a consequence of the normalization lemma.
Notes
References
- M. Atiyah, I.G. Macdonald, Introduction to Commutative Algebra, Addison–Wesley, 1994. ISBN 0-201-40751-5
- James Milne, Algebraic Geometry
 . Let
. Let ![A=k[t_{1},...,t_{n}]](/2014-wikipedia_en_all_02_2014/I/media/8/a/0/4/8a0424814936862d5a4de037692b90bd.png) and
and  be the natural surjection. By the lemma,
be the natural surjection. By the lemma,  and then for any
and then for any 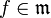 ,
,
 ;
; is a zero of
is a zero of