Yoshio Koide
Yoshio Koide (小出 義夫 Koide Yoshio, born May 16, 1942 in Kanazawa, Ishikawa) is a Japanese theoretical physicist specializing in particle physics. Koide is famous for his eponymous Koide formula, which some physicists think has great importance while other physicists contend that the formula is merely a numerical coincidence.
Koide earned in 1967 a B.Sc. with major in physics and in 1967 a M.Sc. in Theoretical Elementary Particle Physics from Kanazawa University. In 1970, he received his Doctor of Science degree from Hiroshima University with a thesis “On the Two-Body Bound State Problem of Dirac Particles”.[1] After working as a postdoc in the physics department of Hiroshima University and then a postdoc in the applied mathematics department of Osaka University, he became, from 1972 to 1973, a Lecturer in the School of Science and Engineering, Kinki University, Osaka. Koide was Assistant Professor (1973-1977) then Associate Professor (1977-1987) of General Education, Shizuoka Women's University, Shizuoka. From April 1987 to March 2007 he was a Professor of Physics at University of Shizuoka, Shizuoka and then retired as professor emeritus. In 1986 he was a visiting professor at the University of Maryland and in 2002 a visiting researcher at CERN. Koide was from April 2007 to March 2009, a guest professor at Research Institute for Higher Education and Practice, Osaka University, then from April 2009 to March 2011 a guest professor and from April 2011 a guest researcher at Osaka University, and from April 2010 a professor, Department of Maskawa Institute, Kyoto Sangyo University, Kyoto.
In the composite model of mesons, Koide's thesis demonstrated that a mass  of a composite particle which consists of the rest masses
of a composite particle which consists of the rest masses 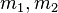 cannot be lighter than
cannot be lighter than  except for the case
except for the case  when JP is not = 0-. This offered a severe problem for the quark model. (Koide’s work was done before the establishment of QCD.)[1]
when JP is not = 0-. This offered a severe problem for the quark model. (Koide’s work was done before the establishment of QCD.)[1]
Katuya and Koide predicted that lifetimes of D± and D0 should be considerably different from what was at that time the conventional anticipation tau(D±)= tau(D0). Their prediction of these lifetimes was the first in the world prior to the experimental observation.[2]
He published the famous Koide formula in 1982[3] with a different presentation in 1983.[4]
Originally, Koide's proposed charged lepton mass formula was based on a composite model of quarks and leptons. In a 1990 paper, from the standpoint that the charged leptons are elementary, by introducing a scalar boson with (octet + singlet) of a family symmetry U(3), Koide re-derived the charged lepton mass formula from minimizing conditions for the scalar potential.[5]
In 2009, he related the neutrino mixing matrix to the up-quark mass matrix.[6]
References
- ↑ 1.0 1.1 Koide, Y. (1968). "On the Two-Body Bound State Problem of Dirac Particles". Progress of Theoretical Physics 39 (3): 817–829. Bibcode:1968PThPh..39..817K. doi:10.1143/PTP.39.817.
- ↑ Katuya, M.; Koide, Y. (1979). "Is the 20-dominance model valid in charm decays, too?". Physical Review D 19: 2631–2634. Bibcode:1979PhRvD..19.2631K. doi:10.1103/PhysRevD.19.2631.
- ↑ Koide, Y. (1982). "Fermion-boson two-body model of quarks and leptons and cabibbo mixing". Lett. Nuovo Cim. 34 (8): 201–205. doi:10.1007/BF02817096.
- ↑ Y. Koide (1983). "A fermion-boson composite model of quarks and leptons". Physics Letters B 120 (1–3): 161–165. Bibcode:1983PhLB..120..161K. doi:10.1016/0370-2693(83)90644-5.
- ↑ Koide, Y. (1990). "Charged Lepton Mass Sum Rule from U(3)-FAMILY Higgs Potential Model". Mod. Phys. Lett. A 5 (28): 2319–2323. Bibcode:1990MPLA....5.2319K. doi:10.1142/S0217732390002663.
- ↑ Koide, Y. (2009). "Yukawaon model in the quark sector and nearly tribimaximal neutrino mixing". Phys. Lett. B 680 (1): 76–80. arXiv:0904.1644. Bibcode:2009PhLB..680...76K. doi:10.1016/j.physletb.2009.08.038.,