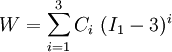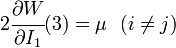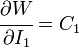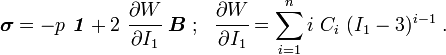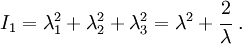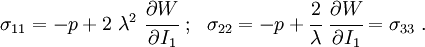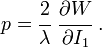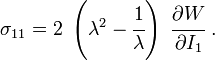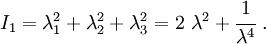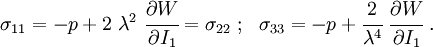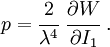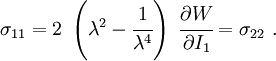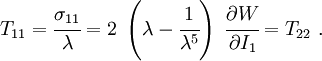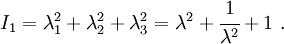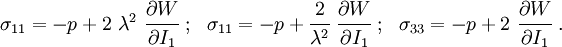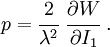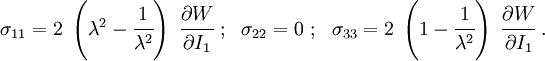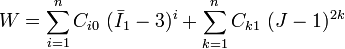Yeoh (hyperelastic model)

From Wikipedia, the free encyclopedia
Yeoh model prediction versus experimental data for natural rubber. Model parameters and experimental data from PolymerFEM.com

The Yeoh hyperelastic material model[1] is a phenomenological model for the deformation of nearly incompressible, nonlinear elastic materials such as rubber. The model is based on Ronald Rivlin's observation that the elastic properties of rubber may be described using a strain energy density function which is a power series in the strain invariants I_{1},I_{2},I_{3}.[2] The Yeoh model for incompressible rubber is a function only of I_{1}. For compressible rubbers, a dependence on 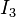I_{3} is added on. Since a polynomial form of the strain energy density function is used but all the three invariants of the left Cauchy-Green deformation tensor are not, the Yeoh model is also called the reduced polynomial model.

Yeoh model for incompressible rubbers

Strain energy density function

The original model proposed by Yeoh had a cubic form with only I_{1} dependence and is applicable to purely incompressible materials. The strain energy density for this model is written as

W=\sum _{{i=1}}^{3}C_{i}~(I_{1}-3)^{i}

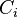where C_{i} are material constants. The quantity 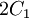2C_{1} can be interpreted as the initial shear modulus.

Today a slightly more generalized version of the Yeoh model is used.[3] This model includes n terms and is written as

W=\sum _{{i=1}}^{n}C_{i}~(I_{1}-3)^{i}~.

When n=1 the Yeoh model reduces to the neo-Hookean model for incompressible materials.

For consistency with linear elasticity the Yeoh model has to satisfy the condition

2{\cfrac {\partial W}{\partial I_{1}}}(3)=\mu ~~(i\neq j)

where \mu is the shear modulus of the material. Now, at I_{1}=3(\lambda _{i}=\lambda _{j}=1),

{\cfrac {\partial W}{\partial I_{1}}}=C_{1}

Therefore, the consistency condition for the Yeoh model is

2C_{1}=\mu \,

Stress-deformation relations

The Cauchy stress for the incompressible Yeoh model is given by

{\boldsymbol {\sigma }}=-p~{\boldsymbol {{\mathit {1}}}}+2~{\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}~;~~{\cfrac {\partial W}{\partial I_{1}}}=\sum _{{i=1}}^{n}i~C_{i}~(I_{1}-3)^{{i-1}}~.

Uniaxial extension

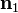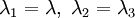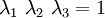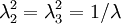For uniaxial extension in the {\mathbf {n}}_{1}-direction, the principal stretches are \lambda _{1}=\lambda ,~\lambda _{2}=\lambda _{3}. From incompressibility \lambda _{1}~\lambda _{2}~\lambda _{3}=1. Hence \lambda _{2}^{2}=\lambda _{3}^{2}=1/\lambda . Therefore,

I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {2}{\lambda }}~.

The left Cauchy-Green deformation tensor can then be expressed as

{\boldsymbol {B}}=\lambda ^{2}~{\mathbf {n}}_{1}\otimes {\mathbf {n}}_{1}+{\cfrac {1}{\lambda }}~({\mathbf {n}}_{2}\otimes {\mathbf {n}}_{2}+{\mathbf {n}}_{3}\otimes {\mathbf {n}}_{3})~.

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

\sigma _{{11}}=-p+2~\lambda ^{2}~{\cfrac {\partial W}{\partial I_{1}}}~;~~\sigma _{{22}}=-p+{\cfrac {2}{\lambda }}~{\cfrac {\partial W}{\partial I_{1}}}=\sigma _{{33}}~.

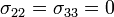Since \sigma _{{22}}=\sigma _{{33}}=0, we have

p={\cfrac {2}{\lambda }}~{\cfrac {\partial W}{\partial I_{1}}}~.

Therefore,

\sigma _{{11}}=2~\left(\lambda ^{2}-{\cfrac {1}{\lambda }}\right)~{\cfrac {\partial W}{\partial I_{1}}}~.

The engineering strain is 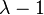\lambda -1\,. The engineering stress is

T_{{11}}=\sigma _{{11}}/\lambda =2~\left(\lambda -{\cfrac {1}{\lambda ^{2}}}\right)~{\cfrac {\partial W}{\partial I_{1}}}~.

Equibiaxial extension

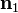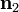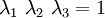For equibiaxial extension in the {\mathbf {n}}_{1} and {\mathbf {n}}_{2} directions, the principal stretches are \lambda _{1}=\lambda _{2}=\lambda \,. From incompressibility \lambda _{1}~\lambda _{2}~\lambda _{3}=1. Hence \lambda _{3}=1/\lambda ^{2}\,. Therefore,

I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=2~\lambda ^{2}+{\cfrac {1}{\lambda ^{4}}}~.

The left Cauchy-Green deformation tensor can then be expressed as

{\boldsymbol {B}}=\lambda ^{2}~{\mathbf {n}}_{1}\otimes {\mathbf {n}}_{1}+\lambda ^{2}~{\mathbf {n}}_{2}\otimes {\mathbf {n}}_{2}+{\cfrac {1}{\lambda ^{4}}}~{\mathbf {n}}_{3}\otimes {\mathbf {n}}_{3}~.

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

\sigma _{{11}}=-p+2~\lambda ^{2}~{\cfrac {\partial W}{\partial I_{1}}}=\sigma _{{22}}~;~~\sigma _{{33}}=-p+{\cfrac {2}{\lambda ^{4}}}~{\cfrac {\partial W}{\partial I_{1}}}~.

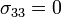Since \sigma _{{33}}=0, we have

p={\cfrac {2}{\lambda ^{4}}}~{\cfrac {\partial W}{\partial I_{1}}}~.

Therefore,

\sigma _{{11}}=2~\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{4}}}\right)~{\cfrac {\partial W}{\partial I_{1}}}=\sigma _{{22}}~.

The engineering strain is 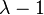\lambda -1\,. The engineering stress is

T_{{11}}={\cfrac {\sigma _{{11}}}{\lambda }}=2~\left(\lambda -{\cfrac {1}{\lambda ^{5}}}\right)~{\cfrac {\partial W}{\partial I_{1}}}=T_{{22}}~.

Planar extension

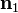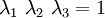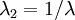Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the {\mathbf {n}}_{1} directions with the {\mathbf {n}}_{3} direction constrained, the principal stretches are \lambda _{1}=\lambda ,~\lambda _{3}=1. From incompressibility \lambda _{1}~\lambda _{2}~\lambda _{3}=1. Hence \lambda _{2}=1/\lambda \,. Therefore,

I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {1}{\lambda ^{2}}}+1~.

The left Cauchy-Green deformation tensor can then be expressed as

{\boldsymbol {B}}=\lambda ^{2}~{\mathbf {n}}_{1}\otimes {\mathbf {n}}_{1}+{\cfrac {1}{\lambda ^{2}}}~{\mathbf {n}}_{2}\otimes {\mathbf {n}}_{2}+{\mathbf {n}}_{3}\otimes {\mathbf {n}}_{3}~.

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

\sigma _{{11}}=-p+2~\lambda ^{2}~{\cfrac {\partial W}{\partial I_{1}}}~;~~\sigma _{{11}}=-p+{\cfrac {2}{\lambda ^{2}}}~{\cfrac {\partial W}{\partial I_{1}}}~;~~\sigma _{{33}}=-p+2~{\cfrac {\partial W}{\partial I_{1}}}~.

Since \sigma _{{22}}=0, we have

p={\cfrac {2}{\lambda ^{2}}}~{\cfrac {\partial W}{\partial I_{1}}}~.

Therefore,

\sigma _{{11}}=2~\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{2}}}\right)~{\cfrac {\partial W}{\partial I_{1}}}~;~~\sigma _{{22}}=0~;~~\sigma _{{33}}=2~\left(1-{\cfrac {1}{\lambda ^{2}}}\right)~{\cfrac {\partial W}{\partial I_{1}}}~.

The engineering strain is 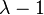\lambda -1\,. The engineering stress is

T_{{11}}={\cfrac {\sigma _{{11}}}{\lambda }}=2~\left(\lambda -{\cfrac {1}{\lambda ^{3}}}\right)~{\cfrac {\partial W}{\partial I_{1}}}~.

Yeoh model for compressible rubbers

A version of the Yeoh model that includes 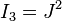I_{3}=J^{2} dependence is used for compressible rubbers. The strain energy density function for this model is written as

W=\sum _{{i=1}}^{n}C_{{i0}}~({\bar {I}}_{1}-3)^{i}+\sum _{{k=1}}^{n}C_{{k1}}~(J-1)^{{2k}}

where {\bar {I}}_{1}=J^{{-2/3}}~I_{1}, and C_{{i0}},C_{{k1}} are material constants. The quantity C_{{10}} is interpreted as half the initial shear modulus, while C_{{11}} is interpreted as half the initial bulk modulus.

When n=1 the compressible Yeoh model reduces to the neo-Hookean model for incompressible materials.

References

  1. ↑ Yeoh, O. H., 1993, "Some forms of the strain energy function for rubber," Rubber Chemistry and technology, Volume 66, Issue 5, November 1993, Pages 754-771.
  2. ↑ Rivlin, R. S., 1948, "Some applications of elasticity theory to rubber engineering", in Collected Papers of R. S. Rivlin vol. 1 and 2, Springer, 1997.
  3. ↑ Selvadurai, A. P. S., 2006, "Deflections of a rubber membrane", Journal of the Mechanics and Physics of Solids, vol. 54, no. 6, pp. 1093-1119.

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.