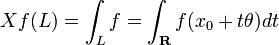X-ray transform

From Wikipedia, the free encyclopedia

In mathematics, the X-ray transform (also called John transform) is an integral transform introduced by Fritz John in 1938^[1] that is one of the cornerstones of modern integral geometry. It is very closely related to the Radon transform, and coincides with it in two dimensions. In higher dimensions, the X-ray transform of a function is defined by integrating over lines rather than over hyperplanes as in the Radon transform. The X-ray transform derives its name from X-ray tomography because the X-ray transform of a function ƒ represents the scattering data of a tomographic scan through an inhomogeneous medium whose density is represented by the function ƒ. Inversion of the X-ray transform is therefore of practical importance because it allows one to reconstruct an unknown density ƒ from its known scattering data.

In detail, if ƒ is a compactly supported continuous function on the Euclidean space Rⁿ, then the X-ray transform of ƒ is the function Xƒ defined on the set of all lines in Rⁿ by

$Xf(L)=\int _{L}f=\int _{{{\mathbf {R}}}}f(x_{0}+t\theta )dt$

where x₀ is an initial point on the line and θ is a unit vector giving the direction of the line L. The latter integral is not regarded in the oriented sense: it is the integral with respect to the 1-dimensional Lebesgue measure on the Euclidean line L.

The X-ray transform satisfies an ultrahyperbolic wave equation called John's equation.

The Gauss hypergeometric function can be written as an X-ray transform (Gelfand, Gindikin & Graev 2003, 2.1.2).

References

↑ Fritz, John (1938). "The ultrahyperbolic differential equation with four independent variables". Duke Mathematical Journal 4: 300–322. doi:10.1215/S0012-7094-38-00423-5. Retrieved 23 January 2013.

Berenstein, Carlos A. (2001), "X-ray transform", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .
Gelfand, I. M.; Gindikin, S. G.; Graev, M. I. (2003) [2000], Selected topics in integral geometry, Translations of Mathematical Monographs 220, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2932-5, MR 2000133
Helgason, Sigurdur (2008), Geometric analysis on symmetric spaces, Mathematical Surveys and Monographs 39 (2nd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4530-1, MR 2463854
Helgason, Sigurdur (1999), The Radon Transform, Progress in Mathematics (2nd ed.), Boston, M.A.: Birkhauser

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.