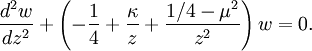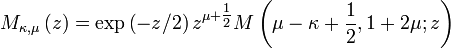Whittaker function

From Wikipedia, the free encyclopedia

In mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by Whittaker (1904) to make the formulas involving the solutions more symmetric. More generally, Jacquet (1966, 1967) introduced Whittaker functions of reductive groups over local fields, where the functions studied by Whittaker are essentially the case where the local field is the real numbers and the group is SL₂(R).

Whittaker's equation is

${\frac {d^{2}w}{dz^{2}}}+\left(-{\frac {1}{4}}+{\frac {\kappa }{z}}+{\frac {1/4-\mu ^{2}}{z^{2}}}\right)w=0.$

It has a regular singular point at 0 and an irregular singular point at ∞. Two solutions are given by the Whittaker functions M_κ,μ(z), W_κ,μ(z), defined in terms of Kummer's confluent hypergeometric functions M and U by

$M_{{\kappa ,\mu }}\left(z\right)=\exp \left(-z/2\right)z^{{\mu +{\tfrac {1}{2}}}}M\left(\mu -\kappa +{\frac {1}{2}},1+2\mu ;z\right)$

$W_{{\kappa ,\mu }}\left(z\right)=\exp \left(-z/2\right)z^{{\mu +{\tfrac {1}{2}}}}U\left(\mu -\kappa +{\frac {1}{2}},1+2\mu ;z\right)$

Whittaker functions appear as coefficients of certain representations of the group SL₂(R), called Whittaker models.

References

Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 13", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, p. 504, ISBN 978-0486612720, MR 0167642 See also chapter 14.
Bateman, Harry (1953), Higher transcendental functions 1, McGraw-Hill .
Brychkov, Yu.A.; Prudnikov, A.P. (2001), "Whittaker function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .
Daalhuis, Adri B. Olde (2010), "Whittaker function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- Jacquet, Hervé (1966), "Une interprétation géométrique et une généralisation P-adique des fonctions de Whittaker en théorie des groupes semi-simples", Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. Séries A et B 262: A943––A945, ISSN 0151-0509, MR 0200390
Jacquet, Hervé (1967), "Fonctions de Whittaker associées aux groupes de Chevalley", Bulletin de la Société Mathématique de France 95: 243–309, ISSN 0037-9484, MR 0271275
Rozov, N.Kh. (2001), "Whittaker equation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .
Slater, Lucy Joan (1960), Confluent hypergeometric functions, Cambridge University Press, MR 0107026 .
Whittaker, Edmund T. (1904), "An expression of certain known functions as generalized hypergeometric functions", Bulletin of the A. M. S. (Providence, R.I.: American Mathematical Society) 10: 125–134

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.