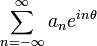Weyl integral

From Wikipedia, the free encyclopedia

Calculus
Fundamental theorem Limits of functions Continuity Mean value theorem Rolle's theorem
Differential calculus Definitions Derivative Differential (infinitesimal) Differential of a function Generalizations of the derivative Concepts Notation for differentiation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem Rules and identities Sums Products Chain rule Powers Quotients Faà di Bruno's formula
Integral calculus Lists of integrals Definitions Antiderivative Integral Improper integral Riemann integral Lebesgue integration Contour integral Integration by parts discs cylindrical shells substitution trigonometric substitution partial fractions changing order reduction formulae
Series Geometric Arithmetico-geometric Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (Term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector calculus Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem Directional derivative
Multivariable calculus Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian
Specialized calculi Calculus of variations Fractional Malliavin Stochastic
v t e

In mathematics, the Weyl integral is an operator defined, as an example of fractional calculus, on functions f on the unit circle having integral 0 and a Fourier series. In other words there is a Fourier series for f of the form

$\sum _{{n=-\infty }}^{{\infty }}a_{n}e^{{in\theta }}$

with a₀ = 0.

Then the Weyl integral operator of order s is defined on Fourier series by

$\sum _{{n=-\infty }}^{{\infty }}(in)^{s}a_{n}e^{{in\theta }}$

where this is defined. Here s can take any real value, and for integer values k of s the series expansion is the expected k-th derivative, if k > 0, or (−k)th indefinite integral normalized by integration from θ = 0.

The condition a₀ = 0 here plays the obvious role of excluding the need to consider division by zero. The definition is due to Hermann Weyl (1917).

References

Lizorkin, P.I. (2001), "Fractional integration and differentiation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Weyl integral

See also

References