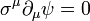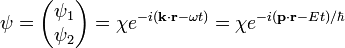Weyl equation

From Wikipedia, the free encyclopedia

Quantum field theory
Feynman diagram
History
Background Field theory Gauge theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking
Symmetries Charge conjugation Crossing Parity Time reversal Symmetry in quantum mechanics
Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Regularization Renormalization Vacuum state Wick's theorem Wightman axioms
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation Bargmann–Wigner equations
Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory
Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything
Scientists C. D. Anderson P. W. Anderson Bethe Bjorken Bogoliubov Brout Callan Coleman DeWitt Dirac Dyson Englert Fermi Feynman Fierz Fock Fröhlich Glashow Gell-Mann Gross Guralnik Heisenberg Higgs Haag Hagen 't Hooft Kendall Kibble Lamb Landau Lee Majorana Mills Nambu Nishijima Parisi Polyakov Salam Schwinger Skyrme Sudarshan Tomonaga Veltman Ward Weinberg Weyl Wilczek Wilson Yang Yukawa
v t e

In physics, particularly quantum field theory, the Weyl Equation is a relativistic wave equation for describing massless spin-1/2 particles. It is named after the German physicist Hermann Weyl.

Equation

The general equation can be written: ^[1]^[2]

$\sigma ^{\mu }\partial _{\mu }\psi =0$

explicitly in SI units:

$I_{2}{\frac {1}{c}}{\frac {\partial \psi }{\partial t}}+\sigma _{x}{\frac {\partial \psi }{\partial x}}+\sigma _{y}{\frac {\partial \psi }{\partial y}}+\sigma _{z}{\frac {\partial \psi }{\partial z}}=0$

where

$\sigma _{\mu }=(\sigma _{0},\sigma _{1},\sigma _{2},\sigma _{3})=(I_{2},\sigma _{x},\sigma _{y},\sigma _{z})$

is a vector whose components is the 2 × 2 identity matrix for μ = 0 and the Pauli matrices for μ = 1,2,3, and ψ is the wavefunction - one of the Weyl spinors.

Weyl spinors

The elements ψ_L and ψ_R are respectively the left and right handed Weyl spinors, each with two components. Both have the form

$\psi ={\begin{pmatrix}\psi _{1}\\\psi _{2}\\\end{pmatrix}}=\chi e^{{-i({\mathbf {k}}\cdot {\mathbf {r}}-\omega t)}}=\chi e^{{-i({\mathbf {p}}\cdot {\mathbf {r}}-Et)/\hbar }}$

where

$\chi ={\begin{pmatrix}\chi _{1}\\\chi _{2}\\\end{pmatrix}}$

is a constant two-component spinor.

Since the particles are massless, i.e. m = 0, the magnitude of momentum p relates directly to the wave-vector k by the De Broglie relations as:

$|{\mathbf {p}}|=\hbar |{\mathbf {k}}|=\hbar \omega /c\,\rightarrow \,|{\mathbf {k}}|=\omega /c$

The equation can be written in terms of left and right handed spinors as:

${\begin{aligned}&\sigma ^{\mu }\partial _{\mu }\psi _{R}=0\\&{\bar {\sigma }}^{\mu }\partial _{\mu }\psi _{L}=0\end{aligned}}$

Helicity

Main article: Helicity (particle physics)

The left and right components correspond to the helicity λ of the particles, the projection of angular momentum operator J onto the linear momentum p:

${\mathbf {p}}\cdot {\mathbf {J}}\left|{\mathbf {p}},\lambda \right\rangle =\lambda |{\mathbf {p}}|\left|{\mathbf {p}},\lambda \right\rangle$

Here $\lambda =\pm 1/2$ .

Derivation

The equations are obtained from the Lagrangian densities

${\mathcal L}=i\psi _{R}^{\dagger }\sigma ^{\mu }\partial _{\mu }\psi _{R}$

${\mathcal L}=i\psi _{L}^{\dagger }{\bar \sigma }^{\mu }\partial _{\mu }\psi _{L}$

By treating the spinor and its conjugate (denoted by $\dagger$ ) as independent variables, the relevant Weyl equation is obtained.

References

↑ Quantum Mechanics, E. Abers, Pearson Ed., Addison Wesley, Prentice Hall Inc, 2004, ISBN 978-0-13-146100-0
↑ The Cambridge Handbook of Physics Formulas, G. Woan, Cambridge University Press, 2010, ISBN 978-0-521-57507-2.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.