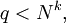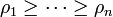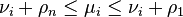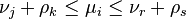Weyl's inequality

From Wikipedia, the free encyclopedia

In mathematics, there are at least two results known as "Weyl's inequality".

Weyl's inequality in number theory

In number theory, Weyl's inequality, named for Hermann Weyl, states that if M, N, a and q are integers, with a and q coprime, q > 0, and f is a real polynomial of degree k whose leading coefficient c satisfies

$|c-a/q|\leq tq^{{-2}},\,$

for some t greater than or equal to 1, then for any positive real number $\scriptstyle \varepsilon$ one has

$\sum _{{x=M}}^{{M+N}}\exp(2\pi if(x))=O\left(N^{{1+\varepsilon }}\left({t \over q}+{1 \over N}+{t \over N^{{k-1}}}+{q \over N^{k}}\right)^{{2^{{1-k}}}}\right){\text{ as }}N\to \infty .$

This inequality will only be useful when

$q<N^{k},\,$

for otherwise estimating the modulus of the exponential sum by means of the triangle inequality as 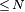$\scriptstyle \leq \,N$ provides a better bound.

Weyl's inequality in matrix theory

In linear algebra, Weyl's inequality is a theorem about the changes to eigenvalues of a Hermitian matrix that is perturbed. It is useful if we wish to know the eigenvalues of the Hermitian matrix H but there is an uncertainty about the entries of H. We let H be the exact matrix and P be a perturbation matrix that represents the uncertainty. The matrix we 'measure' is $\scriptstyle M\,=\,H\,+\,P$ .

The theorem says that if M, H and P are all n by n Hermitian matrices, where M has eigenvalues

$\mu _{1}\geq \cdots \geq \mu _{n}\,$

and H has eigenvalues

$\nu _{1}\geq \cdots \geq \nu _{n}\,$

and P has eigenvalues

$\rho _{1}\geq \cdots \geq \rho _{n}\,$

then the following inequalties hold for 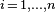$\scriptstyle i\,=\,1,\dots ,n$ :

$\nu _{i}+\rho _{n}\leq \mu _{i}\leq \nu _{i}+\rho _{1}\,$

More generally, if $\scriptstyle j+k-n\,\geq \,i\,\geq \,r+s-1,\dots ,n$ , we have

$\nu _{j}+\rho _{k}\leq \mu _{i}\leq \nu _{r}+\rho _{s}\,$

If P is positive definite (that is, 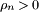$\scriptstyle \rho _{n}\,>\,0$ ) then this implies

$\mu _{i}>\nu _{i}\quad \forall i=1,\dots ,n.\,$

Note that we can order the eigenvalues because the matrices are Hermitian and therefore the eigenvalues are real.

References

Matrix Theory, Joel N. Franklin, (Dover Publications, 1993) ISBN 0-486-41179-6

"Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen", H. Weyl, Math. Ann., 71 (1912), 441–479

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.