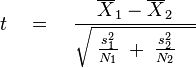Welch's t test
In statistics, Welch's t test is an adaptation of Student's t-test intended for use with two samples having possibly unequal variances.[1] As such, it is an approximate solution to the Behrens–Fisher problem.
Formulas
Welch's t-test defines the statistic t by the following formula:
where  ,
, 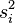 and
and  are the
are the  th sample mean, sample variance and sample size, respectively. Unlike in Student's t-test, the denominator is not based on a pooled variance estimate.
th sample mean, sample variance and sample size, respectively. Unlike in Student's t-test, the denominator is not based on a pooled variance estimate.
The degrees of freedom  associated with this variance estimate is approximated using the Welch–Satterthwaite equation:
associated with this variance estimate is approximated using the Welch–Satterthwaite equation:
Here  =
=  , the degrees of freedom associated with the
, the degrees of freedom associated with the  th variance estimate.
th variance estimate.
Statistical test
Once t and  have been computed, these statistics can be used with the t-distribution to test the null hypothesis that the two population means are equal (using a two-tailed test), or the null hypothesis that one of the population means is greater than or equal to the other (using a one-tailed test). In particular, the test will yield a p-value which might or might not give evidence sufficient to reject the null hypothesis.
have been computed, these statistics can be used with the t-distribution to test the null hypothesis that the two population means are equal (using a two-tailed test), or the null hypothesis that one of the population means is greater than or equal to the other (using a one-tailed test). In particular, the test will yield a p-value which might or might not give evidence sufficient to reject the null hypothesis.
References
- ↑ Welch, B. L. (1947). "The generalization of "Student's" problem when several different population variances are involved". Biometrika 34 (1–2): 28–35. doi:10.1093/biomet/34.1-2.28. MR 19277.
- Further reading
- Daniel Borcard, Lecture Note Appendix: t-test with Welch correction, excerpt from Legendre, P. and D. Borcard. Statistical comparison of univariate tests of homogeneity of variances.
- Sawilowsky, Shlomo S. (2002). "Fermat, Schubert, Einstein, and Behrens–Fisher: The Probable Difference Between Two Means When σ1 ≠ σ2". Journal of Modern Applied Statistical Methods 1 (2): 461–472.