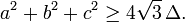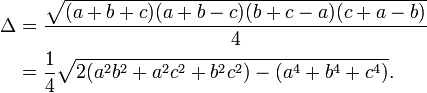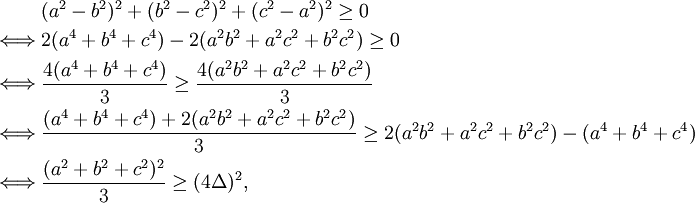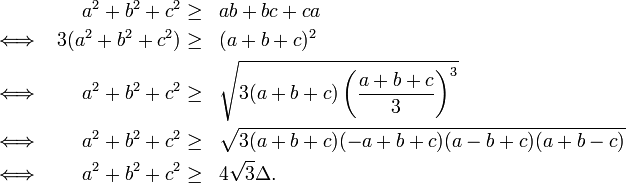Weitzenböck's inequality

From Wikipedia, the free encyclopedia

Not to be confused with Weitzenböck identity.

According to Weitzenböck's inequality, the area of this triangle is at most

(a 2 + b 2 + c 2) ⁄ 4\sqrt 3 .

In mathematics, Weitzenböck's inequality, named after Roland Weitzenböck, states that for a triangle of side lengths $a$ , $b$ , $c$ , and area $\Delta$ , the following inequality holds:

$a^{2}+b^{2}+c^{2}\geq 4{\sqrt {3}}\,\Delta .$

Equality occurs if and only if the triangle is equilateral. Pedoe's inequality is a generalization of Weitzenböck's inequality.

Proofs

The proof of this inequality was set as a question in the International Mathematical Olympiad of 1961. Even so, the result is not too difficult to derive using Heron's formula for the area of a triangle:

${\begin{aligned}\Delta &{}={\frac {{\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}}{4}}\\&{}={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}.\end{aligned}}$

First method

This method assumes no knowledge of inequalities except that all squares are nonnegative.

${\begin{aligned}{}&(a^{2}-b^{2})^{2}+(b^{2}-c^{2})^{2}+(c^{2}-a^{2})^{2}\geq 0\\{}\iff &2(a^{4}+b^{4}+c^{4})-2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})\geq 0\\{}\iff &{\frac {4(a^{4}+b^{4}+c^{4})}{3}}\geq {\frac {4(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})}{3}}\\{}\iff &{\frac {(a^{4}+b^{4}+c^{4})+2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})}{3}}\geq 2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\\{}\iff &{\frac {(a^{2}+b^{2}+c^{2})^{2}}{3}}\geq (4\Delta )^{2},\end{aligned}}$

and the result follows immediately by taking the positive square root of both sides. From the first inequality we can also see that equality occurs only when 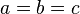$a=b=c$ and the triangle is equilateral.

Second method

This proof assumes knowledge of the rearrangement inequality and the arithmetic-geometric mean inequality.

${\begin{aligned}&&a^{2}+b^{2}+c^{2}&\geq &&ab+bc+ca\\\iff &&3(a^{2}+b^{2}+c^{2})&\geq &&(a+b+c)^{2}\\\iff &&a^{2}+b^{2}+c^{2}&\geq &&{\sqrt {3(a+b+c)\left({\frac {a+b+c}{3}}\right)^{3}}}\\\iff &&a^{2}+b^{2}+c^{2}&\geq &&{\sqrt {3(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\\\iff &&a^{2}+b^{2}+c^{2}&\geq &&4{\sqrt 3}\Delta .\end{aligned}}$

As we have used the rearrangement inequality and the arithmetic-geometric mean inequality, equality only occurs when 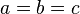$a=b=c$ and the triangle is equilateral.

Third method

It can be shown that the area of the inner Napoleon's triangle is:

${\frac {1}{6}}(a^{2}+b^{2}+c^{2}-4{\sqrt {3}}\,\Delta )$

and therefore greater than or equal to 0.

External links

Weisstein, Eric W., "Weitzenböck's Inequality", MathWorld.
"Weitzenböck's Inequality," an interactive demonstration by Jay Warendorff - Wolfram Demonstrations Project.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.