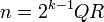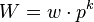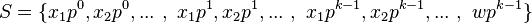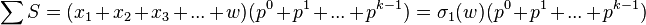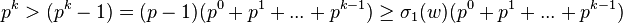Weird number

From Wikipedia, the free encyclopedia

In number theory, a weird number is a natural number that is abundant but not semiperfect.^[1]^[2] In other words, the sum of the proper divisors (divisors including 1 but not itself) of the number is greater than the number, but no subset of those divisors sums to the number itself.

Examples

The smallest weird number is 70. Its proper divisors are 1, 2, 5, 7, 10, 14, and 35; these sum to 74, but no subset of these sums to 70. The number 12, for example, is abundant but not weird, because the proper divisors of 12 are 1, 2, 3, 4, and 6, which sum to 16; but 2+4+6 = 12.

The first few weird numbers are

70, 836, 4030, 5830, 7192, 7912, 9272, 10430, ... (sequence A006037 in OEIS).

Properties

List of unsolved problems in mathematics
Are there any odd weird numbers?

It has been shown that an infinite number of weird numbers exist; in fact, the sequence of weird numbers has positive asymptotic density.^[3]

It is not known if any odd weird numbers exist; if any do, they must be greater than 2³² ≈ 4×10⁹.^[4]

Sidney Kravitz has shown that if k is a positive integer, Q is a prime, and

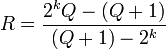$R={\frac {2^{k}Q-(Q+1)}{(Q+1)-2^{k}}}$ ;

if R is prime, then

$n=2^{{k-1}}QR$

is a weird number.^[5] With this formula, he found a large weird number

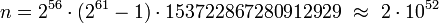$n=2^{{56}}\cdot (2^{{61}}-1)\cdot 153722867280912929\ \approx \ 2\cdot 10^{{52}}$ .

Alternatively, a larger weird number can be calculated using the formula

$W=w\cdot p^{{k}}$

where w is a weird number, p is a prime greater than the sum of divisors of w, and k is any positive integer.

Proof: If the set of divisors of w have a sum greater than w, then the set of divisors of w each multiplied by p^k have a sum greater than wp^k. Divisors of w each multiplied by p^k are all divisors of W, therefore W is abundant.

Assume a subset of proper divisors of W has a sum of W:

$\sum D=d1+d2+d3+...=W$

Let S be the set of divisors of W not divisible by p^k. Let X be the set of divisors of w.

$S=\{x_{{1}}p^{{0}},x_{{2}}p^{{0}},...\ ,\ x_{{1}}p^{{1}},x_{{2}}p^{{1}},...\ ,\ x_{{1}}p^{{k-1}},x_{{2}}p^{{k-1}},...\ ,\ wp^{{k-1}}\}$

Factor the sum:

$\sum S=(x_{{1}}+x_{{2}}+x_{{3}}+...+w)(p^{{0}}+p^{{1}}+...+p^{{k-1}})=\sigma _{{1}}(w)(p^{{0}}+p^{{1}}+...+p^{{k-1}})$

Knowing that p is greater than the sum of divisors of w:

$p^{{k}}>(p^{{k}}-1)=(p-1)(p^{{0}}+p^{{1}}+...+p^{{k-1}})\geq \sigma _{{1}}(w)(p^{{0}}+p^{{1}}+...+p^{{k-1}})$

Therefore no subset of S has a sum divisible by p^k. All other divisors of W are divisible by p^k, therefore all elements of D are divisible by p^k. Dividing both sides of the first equation by p^k results in a subset of proper divisors of w with a sum of w, which is a contradiction if w is weird. Therefore there is no set of proper divisors of W with a sum of W and W is weird.

In popular culture

The Boards of Canada album Geogaddi contains a song titled "The Smallest Weird Number," a reference to another song, "Sixtyten" (equalling 70), as well as their record label, Music70. Despite the song having a running time of 1:17, the audio cuts out at exactly 1:10 (70 seconds).

References

↑ Benkoski, Stan (Aug.-September 1972). "E2308 (in Problems and Solutions)". The American Mathematical Monthly 79 (7): 774. doi:10.2307/2316276. JSTOR 2316276. Check date values in: |date= (help)
↑ Richard K. Guy (2004). Unsolved Problems in Number Theory. Springer-Verlag. ISBN 0-387-20860-7. OCLC 54611248. Section B2.
↑ Benkoski, Stan; Paul Erdős (April 1974). "On Weird and Pseudoperfect Numbers". Mathematics of Computation 28 (126): 617–623. doi:10.2307/2005938. MR 347726. Zbl 0279.10005. Cite uses deprecated parameters (help)
↑ CN Friedman, "Sums of Divisors and Egyptian Fractions", Journal of Number Theory (1993). The result is attributed to "M. Mossinghoff at University of Texas - Austin".
↑ Kravitz, Sidney (1976). "A search for large weird numbers". Journal of Recreational Mathematics (Baywood Publishing) 9 (2): 82–85. Zbl 0365.10003.

External links

Weisstein, Eric W., "Weird number", MathWorld.

v t e Divisibility-based sets of integers

Overview	Integer factorization Divisor Unitary divisor Divisor function Prime factor Fundamental theorem of arithmetic Arithmetic number

Factorization forms	Prime number Composite number Semiprime number Pronic number Sphenic number Square-free number Powerful number Perfect power Achilles number Smooth number Regular number Rough number Unusual number

Constrained divisor sums	Perfect number Almost perfect number Quasiperfect number Multiply perfect number Hemiperfect number Hyperperfect number Superperfect number Unitary perfect number Semiperfect number Practical number

With many divisors	Abundant number Primitive abundant number Highly abundant number Superabundant number Colossally abundant number Highly composite number Superior highly composite number Weird number

Aliquot sequence-related	Untouchable number Amicable number Sociable number Betrothed number

Other sets	Deficient number Friendly number Solitary number Sublime number Harmonic divisor number Frugal number Equidigital number Extravagant number

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.