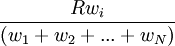Weighted fair queuing
Weighted fair queuing (WFQ) is a data packet scheduling technique allowing different scheduling priorities to statistically multiplexed data flows.
WFQ is a generalization of fair queuing (FQ). Both in WFQ and FQ, each data flow has a separate FIFO queue. In FQ, with a link data rate of  , at any given time the
, at any given time the  active data flows (the ones with non-empty queues) are serviced simultaneously, each at an average data rate of
active data flows (the ones with non-empty queues) are serviced simultaneously, each at an average data rate of  . Since each data flow has its own queue, an ill-behaved flow (who has sent larger packets or more packets per second than the others since it became active) will only punish itself and not other sessions.
. Since each data flow has its own queue, an ill-behaved flow (who has sent larger packets or more packets per second than the others since it became active) will only punish itself and not other sessions.
As opposed to FQ, WFQ allows different sessions to have different service shares. If  data flows currently are active, with weights
data flows currently are active, with weights  data flow number
data flow number  will achieve an average data rate of
will achieve an average data rate of
It can be proven that when using a network with WFQ switches and a data flow that is leaky bucket constrained, an end-to-end delay bound can be guaranteed.[1] By regulating the WFQ weights dynamically, WFQ can be utilized for controlling the quality of service, for example to achieve guaranteed data rate.
Proportional fairness can be achieved by setting the weights to 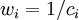 , where
, where  is the cost per data bit of data flow
is the cost per data bit of data flow  . For example in CDMA spread spectrum cellular networks, the cost may be the required energy (the interference level), and in dynamic channel allocation systems, the cost may be the number of nearby base station sites that can not use the same frequency channel, in view to avoid co-channel interference.
. For example in CDMA spread spectrum cellular networks, the cost may be the required energy (the interference level), and in dynamic channel allocation systems, the cost may be the number of nearby base station sites that can not use the same frequency channel, in view to avoid co-channel interference.
See also
- Statistical multiplexing
- Computing scheduling disciplines
- Scheduling algorithm
- Deficit round robin
- Weighted round robin
- Fair Queuing
- Max-min fairness
- Proportional fairness
References
- ↑ Stiliadis, D.; Varma, A. (1998). "Latency-rate servers: A general model for analysis of traffic scheduling algorithms". IEEE/ACM Transactions on Networking 6 (5): 611. doi:10.1109/90.731196.