Webbed space

From Wikipedia, the free encyclopedia

In mathematics, particularly in functional analysis, a webbed space is a topological vector space designed with the goal of allowing the results of the open mapping theorem and the closed graph theorem to hold for a wider class of linear maps. A space is called webbed if there exists a collection of sets, called a web that satisfies certain properties. Webs were first investigated by de Wilde.

Web

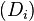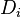Let X be a Hausdorff locally convex topological vector space. A web is a stratified collection of disks satisfying the following absorbency and convergence requirements. The first stratum must consist of a sequence of disks in X, denoted by $(D_{i})$ , such that $X=\cup _{{i}}D_{i}$ . 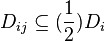For each disk $D_{i}$ in the first stratum, there must exists a sequence of disks in X, denote by $(D_{{ij}})$ such that $D_{{ij}}\subseteq ({\frac {1}{2}})D_{i}$ and $\cup _{{j}}D_{{ij}}$ absorbs $D_{i}$ . 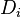This sequence of sequences will form the second stratum. To each disk in the second stratum we assign another sequence of disks with analogously defined properties. This process continuous for countably many strata.

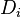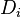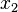A strand is a sequence of disks, with the first disk being selected from the first stratum, say $D_{i}$ , and the second being selected from the sequence that was associated with $D_{i}$ , and so on. We also require that if a sequence of vectors $(x_{n})$ is selected from a strand (with $x_{1}$ belonging to the first disk in the strand, $x_{2}$ belonging to the second, and so on) then the series 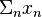$\Sigma _{{n}}x_{n}$ converges.

Webbed space

A Hausdorff locally convex topological vector space on which a web can be defined is called a webbed space.

Examples

Frechet spaces are exactly the webbed spaces with the Baire property.
Projective limits and inductive limits of sequences of webbed spaces are webbed.
The bornologification of a webbed space is webbed.
If X is a metrizable locally convex space then the continuous dual space of X with the strong topology $\beta (X^{*},X)$ is webbed.
If X is the strict inductive limit of a denumerable familiy of metrizable locally convex spaces, then the continuous dual space of X with the strong topology is webbed.
- So in particular, the strong duals of metrizable locally convex spaces are webbed.

Theorems

Closed graph theorem: Any closed linear map from the inductive limit of Baire locally convex spaces into a webbed locally convex space is continuous.
Open mapping theorem: Any continuous surjective linear map from a webbed locally convex space into an inductive limit of Baire locally convex spaces is open.

If the spaces are not locally convex, then there is a notion of web where the requirement of being a disk is replaced by the requirement of being balanced. For such a notion of web we have the following results:

Closed graph theorem: Any closed linear map from the inductive limit of Baire topological vector spaces into a webbed topological vector space is continuous.

References

Lawrence Narici, Edward Beckenstein (1985). Topological Vector Spaces, Second Edition (Chapman & Hall/CRC Pure and Applied Mathematics). Amsterdam: CRC Press. pp. 320–325. ISBN 0824773152.

Kriegl, Andreas; Michor, Peter W. (1997). The Convenient Setting of Global Analysis. Mathematical Surveys and Monographs. American Mathematical Society. pp. 557 – 578. ISBN 9780821807804.

v t e Functional analysis

Local Notions on Sets	Absolutely convex Absorbing Balanced Bounded Cones (Linear, Convex cone) Convex Radial Star-shaped Symmetric

Types of TVSs	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (Tame) Hilbert LF Locally convex Mackey Montel Nuclear Normed (Norm) Reflexive Riesz Smith Stereotype Topological tensor product (of Hilbert spaces) Webbed

Spaces of Maps	Dual space Dual topology Operator topologies Strong Topology (Polar, Operator) Topology of uniform convergence Weak topology (operator) Ultrastrong topology Ultraweak topology

Types of Linear operators	Adjoint Bilinear (form) Bounded (Unbounded) Closed Continuous (Discontinuous) Compact Fredholm Hilbert–Schmidt Functionals (Positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Operations on Sets	Algebraic interior (core) Interior Minkowski addition Polar

Banach Algebras	C-algebras Spectrum (of a C-algebra, Spectral radius) Spectral theory

Important Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (Hyperplane separation) Kakutani fixed-point Lomonosov's Invariant Subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Derivatives (Fréchet derivative, Gâteaux derivative, Functional, Holomorphy) Differentiation in Fréchet spaces Integrals (Bochner, Dunford, Gelfand–Pettis, Regulated, Weak) Functional calculus Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Webbed space

Web

Webbed space

Examples

Theorems

See also

References