Weakly contractible

From Wikipedia, the free encyclopedia

In mathematics, a topological space is said to be weakly contractible if all of its homotopy groups are trivial.

Property

It follows from Whitehead's Theorem that if a CW-complex is weakly contractible then it is contractible.

Example

Define 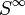$S^{\infty }$ to be the inductive limit of the spheres 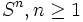$S^{n},n\geq 1$ . Then this space is weakly contractible. Since 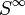$S^{\infty }$ is moreover a CW-complex, it is also contractible. See Contractibility of unit sphere in Hilbert space for more.

References

Hazewinkel, Michiel, ed. (2001), "Homotopy type", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.