Weak base
| Acids and bases |
|---|
 |
| Acid types |
|
| Base types |
In chemistry, a weak base is a chemical base that does not ionize fully in an aqueous solution. As Brønsted–Lowry bases are proton acceptors, a weak base may also be defined as a chemical base in which protonation is incomplete. This results in a relatively low pH compared to strong bases. Bases range from a pH of greater than 7 (7 is neutral, like pure water) to 14 (though some bases are greater than 14). pH has the formula:
Since bases are proton acceptors, the base receives a hydrogen ion from water, H2O, and the remaining H+ concentration in the solution determines pH. Weak bases will have a higher H+ concentration because they are less completely protonated than stronger bases and, therefore, more hydrogen ions remain in the solution. If you plug in a higher H+ concentration into the formula, a low pH results. However, pH of bases is usually calculated using the OH- concentration to find the pOH first. This is done because the H+ concentration is not a part of the reaction, while the OH- concentration is.
By multiplying a conjugate acid (such as NH4+) and a conjugate base (such as NH3) the following is given:
Since ![{K_{w}}=[H_{3}O^{+}][OH^{-}]](/2014-wikipedia_en_all_02_2014/I/media/8/f/f/f/8fff92ca2d3439b5512eae04c9c8fea1.png) then,
then, 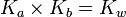
By taking logarithms of both sides of the equation, the following is reached:
Finally, multiplying throughout the equation by -1, the equation turns into:
After acquiring pOH from the previous pOH formula, pH can be calculated using the formula pH = pKw - pOH where pKw = 14.00.
Weak bases exist in chemical equilibrium much in the same way as weak acids do, with a base dissociation constant (Kb) indicating the strength of the base. For example, when ammonia is put in water, the following equilibrium is set up:
Bases that have a large Kb will ionize more completely and are thus stronger bases. As stated above, pH of the solution depends on the H+ concentration, which is related to the OH- concentration by the self-ionization constant (Kw = 1.0x10−14). A strong base has a lower H+ concentration because they are fully protonated and less hydrogen ions remain in the solution. A lower H+ concentration also means a higher OH- concentration and therefore, a larger Kb.
NaOH (s) (sodium hydroxide) is a stronger base than (CH3CH2)2NH (l) (diethylamine) which is a stronger base than NH3 (g) (ammonia). As the bases get weaker, the smaller the Kb values become.
Percentage protonated
As seen above, the strength of a base depends primarily on pH. To help describe the strengths of weak bases, it is helpful to know the percentage protonated-the percentage of base molecules that have been protonated. A lower percentage will correspond with a lower pH because both numbers result from the amount of protonation. A weak base is less protonated, leading to a lower pH and a lower percentage protonated.
The typical proton transfer equilibrium appears as such:
B represents the base.
In this formula, [B]initial is the initial molar concentration of the base, assuming that no protonation has occurred.
A typical pH problem
Calculate the pH and percentage protonation of a .20 M aqueous solution of pyridine, C5H5N. The Kb for C5H5N is 1.8 x 10−9.
First, write the proton transfer equilibrium:
The equilibrium table, with all concentrations in moles per liter, is
| C5H5N | C5H6N+ | OH- | |
|---|---|---|---|
| initial normality | .20 | 0 | 0 |
| change in normality | -x | +x | +x |
| equilibrium normality | .20 -x | x | x |
| Substitute the equilibrium molarities into the basicity constant | 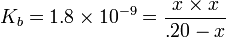 |
| We can assume that x is so small that it will be meaningless by the time we use significant figures. |  |
| Solve for x. | 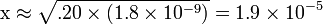 |
| Check the assumption that x << .20 | 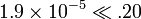 ; so the approximation is valid ; so the approximation is valid |
| Find pOH from pOH = -log [OH-] with [OH-]=x | 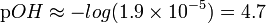 |
| From pH = pKw - pOH, | 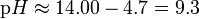 |
| From the equation for percentage protonated with [HB+] = x and [B]initial = .20, |  |
This means .0095% of the pyridine is in the protonated form of C5H5NH+.
Examples
- Alanine,
- Ammonia, NH3
- Methylamine, CH3NH2], C5H8O2
Other weak bases are essentially any bases not on the list of strong bases.
See also
- Strong base
- Weak acid
References
- Atkins, Peter, and Loretta Jones. Chemical Principles: The Quest for Insight, 3rd Ed., New York: W.H. Freeman, 2005.
External links
- Explanation of strong and weak bases from ChemGuide
- Guide to Weak Bases from Georgetown course notes
- Article on Acidity of Solutions of Weak Bases from Intute
![{\mbox{pH}}=-\log _{{10}}\left[{\mbox{H}}^{+}\right]](/2014-wikipedia_en_all_02_2014/I/media/f/5/2/7/f527ad48b384c4a6f2328ab8a42a971f.png)
![{\mbox{pOH}}=-\log _{{10}}\left[{\mbox{OH}}^{-}\right]](/2014-wikipedia_en_all_02_2014/I/media/a/c/7/b/ac7b52a8f87104b49e536517a397e1df.png)
![K_{a}\times K_{b}={[H_{3}O^{+}][NH_{3}] \over [NH_{4}^{+}]}\times {[NH_{4}^{+}][OH^{-}] \over [NH_{3}]}=[H_{3}O^{+}][OH^{-}]](/2014-wikipedia_en_all_02_2014/I/media/1/4/c/f/14cf0b9c22142396e60185078497a046.png)
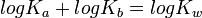
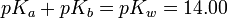
![{\mathrm {K_{b}={[NH_{4}^{+}][OH^{-}] \over [NH_{3}]}}}](/2014-wikipedia_en_all_02_2014/I/media/0/e/b/8/0eb8a1134449c8ec65872d591d4f306a.png)

![Percentage\ protonated={molarity\ of\ HB^{+} \over \ initial\ molarity\ of\ B}\times 100\%={[{HB}^{+}] \over [B]_{{initial}}}{\times 100\%}](/2014-wikipedia_en_all_02_2014/I/media/4/2/9/e/429e42c38e12f6306fdfe7023b5bb11c.png)
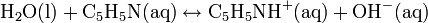
![K_{b}={\mathrm {[C_{5}H_{5}NH^{+}][OH^{-}] \over [C_{5}H_{5}N]}}](/2014-wikipedia_en_all_02_2014/I/media/2/e/7/8/2e78271894ff37cd17623727cf1583f1.png)