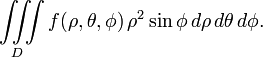Volume integral

From Wikipedia, the free encyclopedia

Calculus
Fundamental theorem Limits of functions Continuity Mean value theorem Rolle's theorem
Differential calculus Definitions Derivative Differential (infinitesimal) Differential of a function Generalizations of the derivative Concepts Notation for differentiation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem Rules and identities Sums Products Chain rule Powers Quotients Faà di Bruno's formula
Integral calculus Lists of integrals Definitions Antiderivative Integral Improper integral Riemann integral Lebesgue integration Contour integral Integration by parts discs cylindrical shells substitution trigonometric substitution partial fractions changing order reduction formulae
Series Geometric Arithmetico-geometric Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (Term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector calculus Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem Directional derivative
Multivariable calculus Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian
Specialized calculi Calculus of variations Fractional Malliavin Stochastic
v t e

In mathematics—in particular, in multivariable calculus—a volume integral refers to an integral over a 3-dimensional domain.

It can also mean a triple integral within a region D in R³ of a function 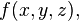$f(x,y,z),$ and is usually written as:

$\iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz.$

A volume integral in cylindrical coordinates is

$\iiint \limits _{D}f(r,\theta ,z)\,r\,dr\,d\theta \,dz,$

and a volume integral in spherical coordinates (using the convention for angles with 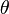$\theta$ as the azimuth and $\phi$ measured from the polar axis (see more on conventions)) has the form

$\iiint \limits _{D}f(\rho ,\theta ,\phi )\,\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi .$

Example 1

Integrating the function 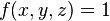$f(x,y,z)=1$ over a unit cube yields the following result:

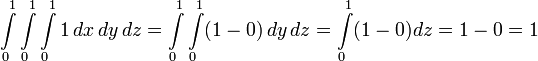
$\int \limits _{0}^{1}\int \limits _{0}^{1}\int \limits _{0}^{1}1\,dx\,dy\,dz=\int \limits _{0}^{1}\int \limits _{0}^{1}(1-0)\,dy\,dz=\int \limits _{0}^{1}(1-0)dz=1-0=1$

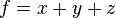So the volume of the unit cube is 1 as expected. This is rather trivial however, and a volume integral is far more powerful. For instance if we have a scalar function ${\begin{aligned}f\colon {\mathbb {R}}^{3}&\to {\mathbb {R}}\end{aligned}}$ describing the density of the cube at a given point $(x,y,z)$ by $f=x+y+z$ then performing the volume integral will give the total mass of the cube:

$\int \limits _{0}^{1}\int \limits _{0}^{1}\int \limits _{0}^{1}\left(x+y+z\right)\,dx\,dy\,dz=\int \limits _{0}^{1}\int \limits _{0}^{1}\left({\frac 12}+y+z\right)\,dy\,dz=\int \limits _{0}^{1}\left(1+z\right)\,dz={\frac 32}$

External links

Hazewinkel, Michiel, ed. (2001), "Multiple integral", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W., "Volume integral", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Volume integral

Example 1

See also

External links