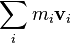Vis viva
In the history of science, vis viva (from the Latin for living force) is an obsolete scientific theory that served as an elementary and limited early formulation of the principle of conservation of energy. It was the first [known] description of what we now call kinetic energy or of energy related to sensible motions.
Proposed by Gottfried Leibniz over the period 1676–1689, the theory was controversial as it seemed to oppose the theory of conservation of momentum advocated by Sir Isaac Newton and René Descartes. The two theories are now understood to be complementary.
The theory was eventually absorbed into the modern theory of energy though the term still survives in the context of celestial mechanics through the vis viva equation.
History
Although ancient philosophers as far back as Thales of Miletus had inklings of the law of conservation of energy[citation needed], it was the German Gottfried Wilhelm Leibniz during 1676–1689 who first attempted a mathematical formulation. Leibniz noticed that in many mechanical systems (of several masses, mi each with velocity vi) the quantity:
was conserved. He called this quantity the vis viva or living force of the system. The principle, it is now realised, represents an accurate statement of the conservation of kinetic energy in elastic collisions, and is a independent of the conservation of momentum. However, many physicists at the time were unaware of this fact and, instead, were influenced by the prestige of Sir Isaac Newton in England and of René Descartes in France, both of whom had set great store by the conservation of momentum as a guiding principle. Thus the momentum:
was held by the rival camp to be the conserved vis viva. It was largely engineers such as John Smeaton, Peter Ewart, Karl Holtzmann, Gustave-Adolphe Hirn and Marc Séguin who objected that conservation of momentum alone was not adequate for practical calculation and who made use of Leibniz's principle. The principle was also championed by some chemists such as William Hyde Wollaston.
The French mathematician Émilie du Châtelet, who had a sound grasp of Newtonian mechanics, developed Leibniz's concept and, combining it with the observations of Willem 's Gravesande, showed that vis viva was dependent on the square of the velocities.
Members of the academic establishment such as John Playfair were quick to point out that kinetic energy is clearly not conserved. This is obvious to a modern analysis based on the second law of thermodynamics but in the 18th and 19th centuries, the fate of the lost energy was still unknown. Gradually it came to be suspected that the heat inevitably generated by motion was another form of vis viva. In 1783, Antoine Lavoisier and Pierre-Simon Laplace reviewed the two competing theories of vis viva and caloric theory. Count Rumford's 1798 observations of heat generation during the boring of cannons added more weight to the view that mechanical motion could be converted into heat. Vis viva now started to be known as energy, after the term was first used in that sense by Thomas Young in 1807.
The recalibration of vis viva to include the coefficient of a half, namely:
was largely the result of the work of Gaspard-Gustave Coriolis and Jean-Victor Poncelet over the period 1819–1839, although present-day definition can occasionally be found earlier (e.g., in Daniel Bernoulli texts).
The former called the quantité de travail (quantity of work) and the latter, travail mécanique (mechanical work) and both championed its use in engineering calculation.
See also
- Conservation of energy: Historical development
- Vis-viva equation
References
- ↑ Bernoulli D. (1741 (1736)). "De legibus quibusdam mechanicis…". Commentarii Academiae scientiarum imperialis Petropolitanae 8: 99–127.
- George E. Smith, "The Vis Viva Dispute: A Controversy at the Dawn of Dynamics", Physics Today 59 (October 2006) Issue 10 pp 31–36. (see also erratum)