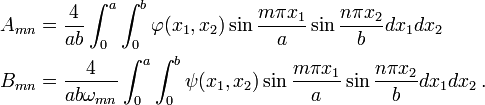Vibration of plates

The vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two. This suggests that a two-dimensional plate theory will give an excellent approximation to the actual three-dimensional motion of a plate-like object, and indeed that is found to be true.[1]
There are several theories that have been developed to describe the motion of plates. The most commonly used are the Kirchhoff-Love theory[2] and the Mindlin-Reissner theory. Solutions to the governing equations predicted by these theories can give us insight into the behavior of plate-like objects both under free and forced conditions. This includes the propagation of waves and the study of standing waves and vibration modes in plates.
Kirchhoff-Love plates
The governing equations for the dynamics of a Kirchhoff-Love plate are
where 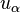 are the in-plane displacements of the mid-surface of the plate,
are the in-plane displacements of the mid-surface of the plate,  is the transverse (out-of-plane) displacement of the mid-surface of the plate,
is the transverse (out-of-plane) displacement of the mid-surface of the plate,  is an applied transverse load, and the resultant forces and moments are defined as
is an applied transverse load, and the resultant forces and moments are defined as
Note that the thickness of the plate is  and that the resultants are defined as weighted averages of the in-plane stresses
and that the resultants are defined as weighted averages of the in-plane stresses  . The derivatives in the governing equations are defined as
. The derivatives in the governing equations are defined as
where the Latin indices go from 1 to 3 while the Greek indices go from 1 to 2. Summation over repeated indices is implied. The 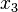 coordinates is out-of-plane while the coordinates
coordinates is out-of-plane while the coordinates  and
and 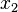 are in plane.
For a uniformly thick plate of thickness
are in plane.
For a uniformly thick plate of thickness  and homogeneous mass density
and homogeneous mass density 
Isotropic Kirchhoff–Love plates
For an isotropic and homogeneous plate, the stress-strain relations are
where  are the in-plane strains. The strain-displacement relations
for Kirchhoff-Love plates are
are the in-plane strains. The strain-displacement relations
for Kirchhoff-Love plates are
Therefore, the resultant moments corresponding to these stresses are
If we ignore the in-plane displacements 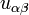 , the governing equations reduce to
, the governing equations reduce to
The above equation can also be written in an alternative notation:
In solid mechanics, a plate is often modeled as a two-dimensional elastic body whose potential energy depends on how it is bent from a planar configuration, rather than how it is stretched (which is the instead the case for a membrane such as a drumhead). In such situations, a vibrating plate can be modeled in a manner analogous to a vibrating drum. However, the resulting partial differential equation for the vertical displacement w of a plate from its equilibrium position is fourth order, involving the square of the Laplacian of w, rather than second order, and its qualitative behavior is fundamentally different from that of the circular membrane drum.
Free vibrations of isotropic plates
For free vibrations, the external force q is zero, and the governing equation of an isotropic plate reduces to
or
This relation can be derived in an alternative manner by considering the curvature of the plate.[3] The potential energy density of a plate depends how the plate is deformed, and so on the mean curvature and Gaussian curvature of the plate. For small deformations, the mean curvature is expressed in terms of w, the vertical displacement of the plate from kinetic equilibrium, as Δw, the Laplacian of w, and the Gaussian curvature is the Monge–Ampère operator wxxwyy−w2
xy. The total potential energy of a plate Ω therefore has the form
apart from an overall inessential normalization constant. Here μ is a constant depending on the properties of the material.
The kinetic energy is given by an integral of the form
Hamilton's principle asserts that w is a stationary point with respect to variations of the total energy T+U. The resulting partial differential equation is
Circular plates
For freely vibrating circular plates, 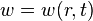 , and the Laplacian in cylindrical coordinates has the form
, and the Laplacian in cylindrical coordinates has the form
Therefore, the governing equation for free vibrations of a circular plate of thickness  is
is
Expanded out,
To solve this equation we use the idea of separation of variables and assume a solution of the form
Plugging this assumed solution into the governing equation gives us
where 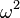 is a constant and
is a constant and 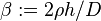 . The solution of the right hand equation is
. The solution of the right hand equation is
The left hand side equation can be written as
where 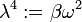 . The general solution of this eigenvalue problem that is
appropriate for plates has the form
. The general solution of this eigenvalue problem that is
appropriate for plates has the form
where  is the order 0 Bessel function of the first kind and
is the order 0 Bessel function of the first kind and  is the order 0 modified Bessel function of the first kind. The constants
is the order 0 modified Bessel function of the first kind. The constants 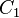 and
and  are determined from the boundary conditions. For a plate of radius
are determined from the boundary conditions. For a plate of radius  with a clamped circumference, the boundary conditions are
with a clamped circumference, the boundary conditions are
From these boundary conditions we find that
We can solve this equation for  (and there are an infinite number of roots) and from that find the modal frequencies
(and there are an infinite number of roots) and from that find the modal frequencies  . We can also express the displacement in the form
. We can also express the displacement in the form
For a given frequency 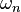 the first term inside the sum in the above equation gives the mode shape. We can find the value
of
the first term inside the sum in the above equation gives the mode shape. We can find the value
of 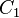 using the appropriate boundary condition at
using the appropriate boundary condition at  and the coefficients
and the coefficients  and
and  from the initial conditions by taking advantage of the orthogonality of Fourier components.
from the initial conditions by taking advantage of the orthogonality of Fourier components.
-

mode n = 1
-
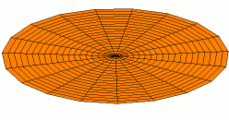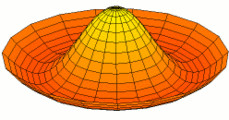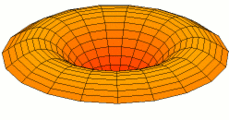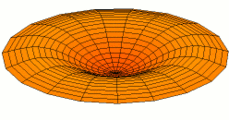
mode n = 2
Rectangular plates
Consider a rectangular plate which has dimensions  in the
in the  -plane and thickness
-plane and thickness  in the
in the 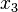 -direction. We seek to find the free vibration modes of the plate.
-direction. We seek to find the free vibration modes of the plate.
Assume a displacement field of the form
Then,
and
Plugging these into the governing equation gives
where 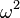 is a constant because the left hand side is independent of
is a constant because the left hand side is independent of  while the right hand side is independent of
while the right hand side is independent of 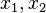 . From the right hand side, we then have
. From the right hand side, we then have
From the left hand side,
where
Since the above equation is a biharmonic eigenvalue problem, we look for Fourier expansion solutions of the form
We can check and see that this solution satisfies the boundary conditions for a freely vibrating rectangular plate with simply supported edges:
Plugging the solution into the biharmonic equation gives us
Comparison with the previous expression for  indicates that we can have an infinite
number of solutions with
indicates that we can have an infinite
number of solutions with
Therefore the general solution for the plate equation is
To find the values of  and
and 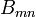 we use initial conditions and the orthogonality of Fourier components. For example, if
we use initial conditions and the orthogonality of Fourier components. For example, if
we get,
References
- ↑ Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis.
- ↑ A. E. H. Love, On the small free vibrations and deformations of elastic shells, Philosophical trans. of the Royal Society (London), 1888, Vol. série A, N° 17 p. 491–549.
- ↑ Courant, Richard; Hilbert, David (1953), Methods of mathematical physics. Vol. I, Interscience Publishers, Inc., New York, N.Y., MR 0065391
See also
- Bending
- Bending of plates
- Infinitesimal strain theory
- Kirchhoff–Love plate theory
- Linear elasticity
- Mindlin–Reissner plate theory
- Plate theory
- Stress (mechanics)
- Stress resultants
- Structural acoustics
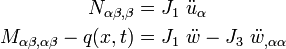
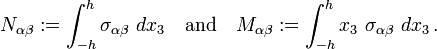

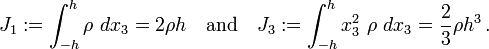
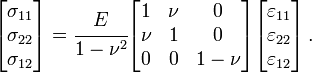
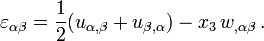

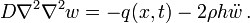
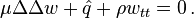
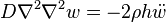
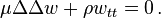
![U=\int _{\Omega }[(\Delta w)^{2}+(1-\mu )(w_{{xx}}w_{{yy}}-w_{{xy}}^{2})]\,dx\,dy](/2014-wikipedia_en_all_02_2014/I/media/7/3/b/c/73bcba61e7f3594251003bf5596a1726.png)



![{\frac {1}{r}}{\frac {\partial }{\partial r}}\left[r{\frac {\partial }{\partial r}}\left\{{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)\right\}\right]=-{\frac {2\rho h}{D}}{\frac {\partial ^{2}w}{\partial t^{2}}}\,.](/2014-wikipedia_en_all_02_2014/I/media/e/d/d/f/eddf1846a20614e2b34a4867d7b88fc9.png)
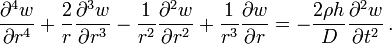
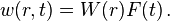
![{\frac {1}{\beta W}}\left[{\frac {d^{4}W}{dr^{4}}}+{\frac {2}{r}}{\frac {d^{3}W}{dr^{3}}}-{\frac {1}{r^{2}}}{\frac {d^{2}W}{dr^{2}}}+{\frac {1}{r^{3}}}{\frac {dW}{dr}}\right]=-{\frac {1}{F}}{\cfrac {d^{2}F}{dt^{2}}}=\omega ^{2}](/2014-wikipedia_en_all_02_2014/I/media/f/b/5/c/fb5cade0825335dae508f9f065c11d4b.png)
![F(t)={\text{Re}}[Ae^{{i\omega t}}+Be^{{-i\omega t}}]\,.](/2014-wikipedia_en_all_02_2014/I/media/b/6/3/e/b63e174d639604b6d2090ff6b9ae1c03.png)

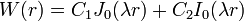

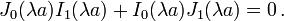
![w(r,t)=\sum _{{n=1}}^{\infty }C_{n}\left[J_{0}(\lambda _{n}r)-{\frac {J_{0}(\lambda _{n}a)}{I_{0}(\lambda _{n}a)}}I_{0}(\lambda _{n}r)\right][A_{n}e^{{i\omega _{n}t}}+B_{n}e^{{-i\omega _{n}t}}]\,.](/2014-wikipedia_en_all_02_2014/I/media/a/d/4/9/ad49d025099f3ad25c971b3cf921a720.png)
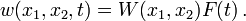
![\nabla ^{2}\nabla ^{2}w=w_{{,1111}}+2w_{{,1212}}+w_{{,2222}}=\left[{\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}\right]F(t)](/2014-wikipedia_en_all_02_2014/I/media/4/e/a/4/4ea44c25c3cd21b0526fc9377af9c5ec.png)

![{\frac {D}{2\rho hW}}\left[{\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}\right]=-{\frac {1}{F}}{\frac {d^{2}F}{dt^{2}}}=\omega ^{2}](/2014-wikipedia_en_all_02_2014/I/media/0/e/2/8/0e28e9795a468bef5ae2194ab58885d4.png)
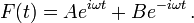

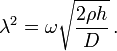
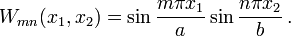


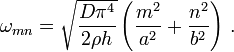
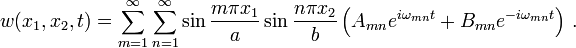
![w(x_{1},x_{2},0)=\varphi (x_{1},x_{2})\quad {\text{on}}\quad x_{1}\in [0,a]\quad {\text{and}}\quad {\frac {\partial w}{\partial t}}(x_{1},x_{2},0)=\psi (x_{1},x_{2})\quad {\text{on}}\quad x_{2}\in [0,b]](/2014-wikipedia_en_all_02_2014/I/media/c/2/a/8/c2a8842910e7915fc1efa5634dcfa8d6.png)