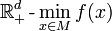Vector optimization
Vector optimization is an optimization problem of simultaneously optimizing multiple objective functions subject to constraints and a given ordering. Any multi-objective optimization problem is a vector optimization problem with the trivial ordering.
Canonical example
In mathematical terms, the vector optimization problem can be written as:
where 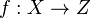 for some vector spaces
for some vector spaces 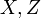 ,
, 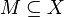 ,
, 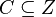 is an ordering cone in
is an ordering cone in  , and
, and  denotes minimizing with respect to the ordering cone.
denotes minimizing with respect to the ordering cone.
The solution to this minimization problem is the smallest set 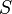 such that for every
such that for every  there exists a
there exists a  where
where 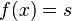 and
and 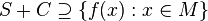 .
.
Solution types
-
 is a weakly efficient point (w-minimizer) if there exists a neighborhood
is a weakly efficient point (w-minimizer) if there exists a neighborhood  around
around  such that for every
such that for every  it follows that
it follows that 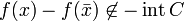 .
. -
 is an efficient point (e-minimizer) if there exists a neighborhood
is an efficient point (e-minimizer) if there exists a neighborhood  around
around  such that for every
such that for every  it follows that
it follows that  .
. -
 is a properly efficient point (p-minimizer) if
is a properly efficient point (p-minimizer) if  is a weakly efficient point with respect to a closed pointed convex cone
is a weakly efficient point with respect to a closed pointed convex cone 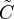 where
where 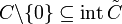 .
.
Every p-minimizer is an e-minimizer. And every e-minimizer is a w-minimizer.[1]
Solution methods
- Benson's algorithm for linear vector optimization problems[2]
Relation to multi-objective optimization
Any multi-objective optimization problem can be written as
where 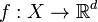 and
and 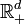 is the positive orthant of
is the positive orthant of  . Thus the solution set of this vector optimization problem is given by the Pareto efficient points.
. Thus the solution set of this vector optimization problem is given by the Pareto efficient points.
References
- ↑ Ginchev, I.; Guerraggio, A.; Rocca, M. (2006). "From Scalar to Vector Optimization". Applications of Mathematics 51: 5. doi:10.1007/s10492-006-0002-1.
- ↑ Andreas Löhne (2011). Vector Optimization with Infimum and Supremum. Springer. ISBN 9783642183508.