Varifold

From Wikipedia, the free encyclopedia

In mathematics, a varifold is, loosely speaking, a measure-theoretic generalization of the concept of a differentiable manifold, by replacing differentiability requirements with those provided by rectifiable sets, while maintaining the general algebraic structure usually seen in differential geometry. More closely, varifolds generalize the ideas of a rectifiable current. Varifolds are the topic of study in geometric measure theory.

Historical note

Varifolds were first introduced by Frederick Almgren in 1964:^[1] he coined the name varifold meaning that these objects are substitutes for ordinary manifolds in problems of the calculus of variations.^[2] The modern approach to the theory was laid down by William Allard, in the paper (Allard 1972).

Definition

Given an open subset $\Omega$ of Euclidean space ℝⁿ, an m-dimensional varifold on $\Omega$ is defined as a Radon measure on the set

$\Omega \times G(n,m)$

where $G(n,m)$ is the Grassmannian of all m-dimensional linear subspaces of an n-dimensional vector space. The Grassmannian is used to allow the construction of analogs to differential forms as duals to vector fields in the approximate tangent space of the set $\Omega$ .

The particular case of a rectifiable varifold is the data of a m-rectifiable set M (which is measurable with respect to the m-dimensional Hausdorff measure), and a density function defined on M, which is a positive function θ measurable and locally integrable with respect to the m-dimensional Hausdorff measure. It defines a Radon measure V on the Grassmannian bundle of ℝⁿ

$V(A):=\int _{{\Gamma _{{M,A}}}}\!\!\!\!\!\!\!\theta (x){\mathrm {d}}{\mathcal {H}}^{m}(x)$

where

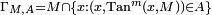
$\scriptstyle \Gamma _{{M,A}}=M\cap \{x:(x,{\mathrm {Tan}}^{m}(x,M))\in A\}$
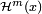$\scriptstyle {\mathcal {H}}^{m}(x)$ is the $m$ −dimensional Hausdorff measure

Rectifiable varifolds are weaker objects than locally rectifiable currents: they do not have any orientation. Replacing M with more regular sets, one easily see that differentiable submanifolds are particular cases of rectifiable manifolds.

Due to the lack of orientation, there is no boundary operator defined on the space of varifolds.

Notes

↑ The first widely circulated exposition of Almgren's ideas is the book (Almgren 1966): however, the first systematic exposition of the theory is contained in the book (Almgren 1965), which had a far lower circulation, even if it is cited in Herbert Federer's classic text on geometric measure theory. See also the brief, clear survey by De Giorgi (1968, p. 400).
↑ Probably the acronym is variational manifold, as Almgren (1993, p. 46) describes the coining of the name with the following exact words:-"I called the objects "varifolds" having in mind that they were a measure-theoretic substitute for manifolds created for the variational calculus."

Historical references

Almgren, Frederick J. Jr. (1993), "Questions and answers about area-minimizing surfaces and geometric measure theory.", in Greene, Robert E.; Yau, S.-T., Differential Geometry. Part 1: Partial Differential Equations on Manifolds. Proceedings of a summer research institute, held at the University of California, Los Angeles, CA, USA, July 8–28, 1990, Proceedings of Symposia in Pure Mathematics 54, Providence, RI: American Mathematical Society, pp. 29–53, ISBN 0-8218-1494-X, MR 1216574, Zbl 0812.49032 . This paper is also reproduced in (Almgren 1999, pp. 497–521).
Almgren, Frederick J. Jr. (1999), Selected works of Frederick J. Almgren, Jr., Collected Works 13, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1067-5, MR 1747253, Zbl 0966.01031 .
De Giorgi, Ennio (1968), "Hypersurfaces of minimal measure in pluridimensional euclidean spaces", in Petrovsky, I. G., Trudy Mezhdunarodnogo kongressa matematikov. Proceedings of International Congress of Mathematicians (Moscow−1966), ICM Proceedings, Moscow: Mir Publishers, pp. 395−401, MR 0234329, Zbl 0188.17503 .

References

Allard, William K. (May 1972), "On the first variation of a varifold", Annals of Mathematics, Second Series 95 (3): 417–491, JSTOR 1970868, MR 0307015, Zbl 0252.49028 .
Allard, William K. (May 1975), "On the first variation of a varifold: Boundary Behavior", Annals of Mathematics, Second Series 101 (3): 418–446, JSTOR 1970934, MR 0397520, Zbl 0319.49026 .
Almgren, Frederick J. Jr. (1965), The theory of varifolds: A variational calculus in the large for the $k$ -dimensional area integrand, Princeton: Princeton University Library, p. 178 . A set of mimeographed notes where Frederick J. Almgren, Jr. introduces varifolds for the first time.
Almgren, Frederick J. Jr. (1966), Plateau's Problem: An Invitation to Varifold Geometry, Mathematics Monographs Series (1st ed.), New York–Amsterdam: W. A. Benjamin, Inc., pp. XII+74, MR 0190856, Zbl 0165.13201 . The first widely circulated book describing the concept of a varifold and its applications to the Plateau's problem, particularly in chapter 4, section 6 "A solution to the existence portion of Plateau's problem".
Almgren, Frederick J. Jr. (2001) [1966], Plateau's Problem: An Invitation to Varifold Geometry, Student Mathematical Library 13 (2nd ed.), Providence, RI: American Mathematical Society, pp. xvi+78, ISBN 978-0-8218-2747-5, MR 1853442, Zbl 0995.49001 . The second edition of the book (Almgren 1966).
Đào, Trọng Thi; Fomenko, A. T. (1991), Minimal Surfaces, Stratified Multivarifolds, and the Plateau Problem, Translations of Mathematical Monographs 84, Providence, RI: American Mathematical Society, pp. ix+404, ISBN 0-8218-4536-5, MR 1093903, Zbl 0716.53003 .
T.C.O'Neil (2001), "Geometric measure theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Simon, Leon (1984), Lectures on Geometric Measure Theory, Proceedings of the Centre for Mathematical Analysis 3, Canberra: Centre for Mathematics and its Applications (CMA), Australian National University, pp. VII+272 (loose errata), ISBN 0-86784-429-9, MR 0756417, Zbl 0546.49019 .
Lin, Fanghua; Yang, Xiaoping (2002), Geometric Measure Theory – An Introduction, Advanced Mathematics (Beijing/Boston) 1, Beijing–New York / Boston, MA: Science Press / International Press, pp. x+237, MR 2030862, Zbl 0546.49019 , ISBN 7-03-010271-1 (Science Press), ISBN 1-57146-125-6 (International Press).

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.