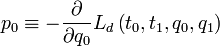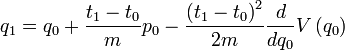Variational integrator

From Wikipedia, the free encyclopedia

Variational integrators are numerical integrators for Hamiltonian systems derived from the Euler-Lagrange equations of a discretized Hamilton's principle. Variational integrators are momentum-preserving and symplectic.

Derivation of a Simple Variational Integrator

Consider a mechanical system with a single particle degree of freedom described by the Lagrangian

$L(t,q,v)={\frac {1}{2}}mv^{2}-V(q)$ ,

where $m$ is the mass of the particle, and $V$ is a potential. To construct a variational integrator for this system, we begin by forming the discrete Lagrangian. The discrete Lagrangian approximates the action for the system over a short time interval:

$L_{d}\left(t_{0},t_{1},q_{0},q_{1}\right)={\frac {t_{1}-t_{0}}{2}}\left[L\left(t_{0},q_{0},{\frac {q_{1}-q_{0}}{t_{1}-t_{0}}}\right)+L\left(t_{1},q_{1},{\frac {q_{1}-q_{0}}{t_{1}-t_{0}}}\right)\right]\approx \int _{{t_{0}}}^{{t_{1}}}dt\,L(t,q(t),v(t))$ .

Here we have chosen to approximate the time integral using the trapezoid method, and we use a linear approximation to the trajectory,

$q(t)\approx {\frac {q_{1}-q_{0}}{t_{1}-t_{0}}}\left(t-t_{0}\right)+q_{0}$

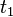between $t_{0}$ and $t_{1}$ , resulting in a constant velocity 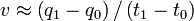$v\approx \left(q_{1}-q_{0}\right)/\left(t_{1}-t_{0}\right)$ . Different choices for the approximation to the trajectory and the time integral give different variational integrators. The order of accuracy of the integrator is controlled by the accuracy of our approximation to the action; since

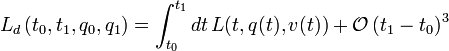$L_{d}\left(t_{0},t_{1},q_{0},q_{1}\right)=\int _{{t_{0}}}^{{t_{1}}}dt\,L(t,q(t),v(t))+{\mathcal {O}}\left(t_{1}-t_{0}\right)^{3}$ ,

our integrator will be second-order accurate.

Evolution equations for the discrete system can be derived from a stationary-action principle. The discrete action over an extended time interval is a sum of discrete Lagrangians over many sub-intervals:

$S_{d}=L_{d}\left(t_{0},t_{1},q_{0},q_{1}\right)+L_{d}\left(t_{1},t_{2},q_{1},q_{2}\right)+\ldots$ .

The principle of stationary action states that the action is stationary with respect to variations of coordinates that leave the endpoints of the trajectory fixed. So, varying the coordinate $q_{1}$ , we have

${\frac {\partial S_{d}}{\partial q_{1}}}=0={\frac {\partial }{\partial q_{1}}}L_{d}\left(t_{0},t_{1},q_{0},q_{1}\right)+{\frac {\partial }{\partial q_{1}}}L_{d}\left(t_{1},t_{2},q_{1},q_{2}\right)$ .

Given an initial condition $(q_{0},q_{1})$ , and a sequence of times 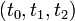$(t_{0},t_{1},t_{2})$ this provides a relation that can be solved for $q_{2}$ . The solution is

$q_{2}=q_{1}+{\frac {t_{2}-t_{1}}{t_{1}-t_{0}}}\left(q_{1}-q_{0}\right)-{\frac {\left(t_{2}-t_{0}\right)\left(t_{2}-t_{1}\right)}{2m}}{\frac {d}{dq_{1}}}V\left(q_{1}\right)$ .

We can write this in a simpler form if we define the discrete momenta,

$p_{0}\equiv -{\frac {\partial }{\partial q_{0}}}L_{d}\left(t_{0},t_{1},q_{0},q_{1}\right)$

and

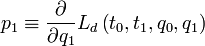$p_{1}\equiv {\frac {\partial }{\partial q_{1}}}L_{d}\left(t_{0},t_{1},q_{0},q_{1}\right)$ .

Given an initial condition 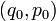$(q_{0},p_{0})$ , the stationary action condition is equivalent to solving the first of these equations for $q_{1}$ , and then determining $p_{1}$ using the second equation. This evolution scheme gives

$q_{1}=q_{0}+{\frac {t_{1}-t_{0}}{m}}p_{0}-{\frac {\left(t_{1}-t_{0}\right)^{2}}{2m}}{\frac {d}{dq_{0}}}V\left(q_{0}\right)$

and

$p_{1}=m{\frac {q_{1}-q_{0}}{t_{1}-t_{0}}}-{\frac {t_{1}-t_{0}}{2}}{\frac {d}{dq_{1}}}V\left(q_{1}\right)$ .

This is a leapfrog integration scheme for the system; two steps of this evolution are equivalent to the formula above for $q_{2}$

References

E. Hairer, C. Lubich, and G. Wanner. Geometric Numerical Integration. Springer, 2002.
J. Marsden and M. West. Discrete mechanics and variational integrators. Acta Numerica, 2001, pp. 357–514.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.