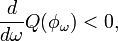Vakhitov–Kolokolov stability criterion

From Wikipedia, the free encyclopedia

The Vakhitov–Kolokolov stability criterion is a condition for linear stability (sometimes called spectral stability) of solitary wave solutions to a wide class of U(1)-invariant Hamiltonian systems, named after Russian scientists Aleksandr Kolokolov (Александр Александрович Колоколов) and Nazib Vakhitov (Назиб Галиевич Вахитов). The condition for linear stability of a solitary wave 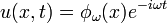u(x,t)=\phi _{\omega }(x)e^{{-i\omega t}}\, with frequency \omega \, has the form

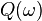{\frac {d}{d\omega }}Q(\omega )<0,

where Q(\omega )\, is the charge (or momentum) of the solitary wave \phi _{\omega }(x)e^{{-i\omega t}}\,, conserved by Noether's theorem due to U(1)-invariance of the system.

Original formulation

Originally, this criterion was obtained for the nonlinear Schrödinger equation,

i{\frac {\partial }{\partial t}}u(x,t)=-{\frac {\partial ^{2}}{\partial x^{2}}}u(x,t)+g(|u(x,t)|^{2})u(x,t),

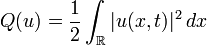where x\in \mathbb{R} \,, t\in \mathbb{R} , and g\in C^{\infty }(\mathbb{R} ) is a smooth real-valued function. The solution u(x,t)\, is assumed to be complex-valued. Since the equation is U(1)-invariant, by Noether's theorem, it has an integral of motion, Q(u)={\frac {1}{2}}\int _{{\mathbb{R} }}|u(x,t)|^{2}\,dx, which is called charge or momentum, depending on the model under consideration. 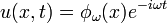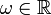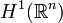For a wide class of functions g\,, the nonlinear Schrödinger equation admits solitary wave solutions of the form u(x,t)=\phi _{\omega }(x)e^{{-i\omega t}}\,, where \omega \in \mathbb{R} and \phi _{\omega }(x)\, decays for large x\, (one often requires that \phi _{\omega }(x)\, belongs to the Sobolev space H^{1}(\mathbb{R} ^{n})). Usually such solutions exist for \omega \, from an interval or collection of intervals of a real line. Vakhitov–Kolokolov stability criterion,[1] [2]

{\frac {d}{d\omega }}Q(\phi _{\omega })<0,

is a condition of spectral stability of a solitary wave solution. Namely, if this condition is satisfied at a particular value of \omega \,, then the linearization at the solitary wave with this \omega \, has no spectrum in the right half-plane.

This result is based on an earlier work[3] by Vladimir Zakharov.

Generalizations

This result has been generalized to abstract Hamiltonian systems with U(1)-invariance .[4] It was shown that under rather general conditions the Vakhitov–Kolokolov stability criterion guarantees not only spectral stability but also orbital stability of solitary waves.

The stability condition has been generalized [5] to traveling wave solutions to the generalized Korteweg–de Vries equation of the form

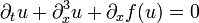\partial _{t}u+\partial _{x}^{3}u+\partial _{x}f(u)=0\,.

The stability condition has also been generalized to Hamiltonian systems with a more general symmetry group .[6]

See also

References

  1. ↑ Вахитов, Н. Г. and Колоколов, А. А. (1973). "Стационарные решения волнового уравнения в среде с насыщением нелинейности". Известия высших учебных заведений. Радиофизика 16: 1020–1028. 
  2. ↑ N.G. Vakhitov and A.A. Kolokolov (1973). "Stationary solutions of the wave equation in the medium with nonlinearity saturation". Radiophys. Quantum Electron. 16: 783–789. Bibcode:1973R%26QE...16..783V. doi:10.1007/BF01031343. 
  3. ↑ Vladimir E. Zakharov (1967). "Instability of Self-focusing of Light". Zh. Eksp. Teor. Fiz 53: 1735–1743. Bibcode:1968JETP...26..994Z. 
  4. ↑ Manoussos Grillakis, Jalal Shatah, and Walter Strauss (1987). "Stability theory of solitary waves in the presence of symmetry. I". J. Funct. Anal. 74: 160–197. doi:10.1016/0022-1236(87)90044-9. 
  5. ↑ Jerry Bona, Panagiotis Souganidis, and Walter Strauss (1987). "Stability and instability of solitary waves of Korteweg-de Vries type". Proceedings of the Royal Society A 411 (1841): 395–412. Bibcode:1987RSPSA.411..395B. doi:10.1098/rspa.1987.0073. 
  6. ↑ Manoussos Grillakis, Jalal Shatah, and Walter Strauss (1990). "Stability theory of solitary waves in the presence of symmetry". J. Funct. Anal. 94: 308–348. doi:10.1016/0022-1236(90)90016-E. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.