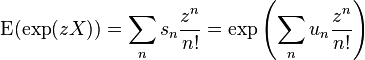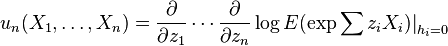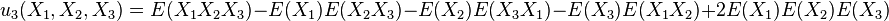Ursell function
In statistical mechanics, an Ursell function or connected correlation function, is a cumulant of a random variable. It is also called a connected correlation function as it can often be obtained by summing over connected Feynman diagrams (the sum over all Feynman diagrams gives the correlation functions).
The Ursell function was named after Harold Ursell, who introduced it in 1927.
Definition
If X is a random variable, the moments sn and cumulants (same as the Ursell functions) un are functions of X related by the exponential formula:
(where E is the expectation).
The Ursell functions for multivariate random variables are defined analogously to the above, and in the same way as multivariate cumulants.[1]
The Ursell functions of a single random variable X are obtained from these by setting X=X1=...=Xn.
The first few are given by
Characterization
Percus (1975) showed that the Ursell functions, considered as multilinear functions of several random variables, are uniquely determined up to a constant by the fact that they vanish whenever the variables Xi can be divided into two nonempty independent sets.
References
- ↑ Shlosman, S. B. (1986). "Signs of the Ising model Ursell functions". Communications in Mathematical Physics 102 (4): 679–686. Bibcode:1985CMaPh.102..679S. doi:10.1007/BF01221652.
- Glimm, James; Jaffe, Arthur (1987), Quantum physics (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96476-8, MR 887102
- Percus, J. K. (1975), "Correlation inequalities for Ising spin lattices", Comm. Math. Phys. 40: 283–308, MR 0378683
- Ursell, H. D. (1927), "The evaluation of Gibbs phase-integral for imperfect gases", Proc. Cambridge Philos. Soc 23: 685–697, doi:10.1017/S0305004100011191