Universal C*-algebra
In mathematics, more specifically in the theory of C*-algebras, a universal C*-algebra is one characterized by a universal property.
A universal C*-algebra can be expressed as a presentation, in terms of generators and relations. One requires that the generators must be realizable as bounded operators on a Hilbert space, and that the relations must prescribe a uniform bound on the norm of each generator. For example, the universal C*-algebra generated by a unitary element u has presentation <u | u*u = uu* = 1>. By the functional calculus, this C*-algebra is the continuous functions on the unit circle in the complex plane. Any C*-algebra generated by a unitary element is the homomorphic image of this universal C*-algebra.
We next describe a general framework for defining a large class of these algebras. Let S be a countable semigroup (in which we denote the operation by juxtaposition) with identity e and with an involution * such that
Define
l1(S) is a Banach space, and becomes an algebra under convolution defined as follows:
l1(S) has a multiplicative identity, viz, the function δe which is zero except at e, where it takes the value 1. It has the involution
Theorem. l1(S) is a B*-algebra with identity.
The universal C*-algebra of contractions generated by S is the C*-enveloping algebra of l1(S). We can describe it as follows: For every state f of l1(S), consider the cyclic representation πf associated to f. Then
is a C*-seminorm on l1(S), where the supremum ranges over states f of l1(S). Taking the quotient space of l1(S) by the two-sided ideal of elements of norm 0, produces a normed algebra which satisfies the C*-property. Completing with respect to this norm, yields a C*-algebra.
References
- Loring, T. (1997), Lifting Solutions to Perturbing Problems in C*-Algebras, Fields Institute Monographs 8, American Mathematical Society, ISBN 0-8218-0602-5
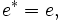
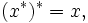
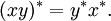

=\sum _{{\{u,v:uv=x\}}}\varphi (u)\psi (v)](/2014-wikipedia_en_all_02_2014/I/media/6/2/a/7/62a7af5b107e8bf9b656ce7f2696ed66.png)

