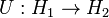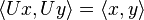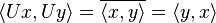Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that preserves the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation.
More precisely, a unitary transformation is an isomorphism between two Hilbert spaces. In other words, a unitary transformation is a bijective function
where 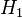 and
and  are Hilbert spaces, such that
are Hilbert spaces, such that
for all  and
and  in
in 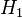 . A unitary transformation is an isometry, as one can see by setting
. A unitary transformation is an isometry, as one can see by setting  in this formula.
in this formula.
In the case when 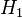 and
and  are the same space, a unitary transformation is an automorphism of that Hilbert space, and then it is also called a unitary operator.
are the same space, a unitary transformation is an automorphism of that Hilbert space, and then it is also called a unitary operator.
A closely related notion is that of antiunitary transformation, which is a bijective function
between two complex Hilbert spaces such that
for all  and
and  in
in 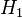 , where the horizontal bar represents the complex conjugate.
, where the horizontal bar represents the complex conjugate.
See also
- Antiunitary
- Orthogonal transformation
- Time reversal
- Unitary group
- Unitary operator
- Unitary matrix
- Wigner's Theorem