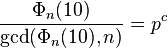Unique prime

From Wikipedia, the free encyclopedia

In number theory, a unique prime is a certain kind of prime number. A prime p ≠ 2, 5 is called unique if there is no other prime q such that the period length of the decimal expansion of its reciprocal, 1 / p, is equivalent to the period length of the reciprocal of q, 1 / q. Unique primes were first described by Samuel Yates in 1980.

It can be shown that a prime p is of unique period n if and only if there exists a natural number c such that

${\frac {\Phi _{n}(10)}{\gcd(\Phi _{n}(10),n)}}=p^{c}$

where Φ_n(x) is the n-th cyclotomic polynomial. At present, more than fifty unique primes or probable primes are known. However, there are only twenty-three unique primes below 10¹⁰⁰. The following table gives an overview of all 23 unique primes below 10¹⁰⁰ (sequence A040017 in OEIS) and their periods (sequence A051627 in OEIS):

Period length	Prime
1	3
2	11
3	37
4	101
10	9,091
12	9,901
9	333,667
14	909,091
24	99,990,001
36	999,999,000,001
48	9,999,999,900,000,001
38	909,090,909,090,909,091
19	1,111,111,111,111,111,111
23	11,111,111,111,111,111,111,111
39	900,900,900,900,990,990,990,991
62	909,090,909,090,909,090,909,090,909,091
120	100,009,999,999,899,989,999,000,000,010,001
150	10,000,099,999,999,989,999,899,999,000,000,000,100,001
106	9,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,091
93	900,900,900,900,900,900,900,900,900,900,990,990,990,990,990,990,990,990,990,991
134	909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,091
294	142,857,157,142,857,142,856,999,999,985,714,285,714,285,857,142,857,142,855,714,285,571,428,571,428,572,857,143
196	999,999,999,999,990,000,000,000,000,099,999,999,999,999,000,000,000,000,009,999,999,999,999,900,000,000,000,001

The prime with period length 294 is similar to the reciprocal of 7 (0.142857142857142857...)

Just after the table, the twenty-fourth unique prime has 128 digits and period length 320. It can be written as (9₃₂0₃₂)₂ + 1, where a subscript number n indicates n consecutive copies of the digit or group of digits before the subscript.

Though they are rare, based on the occurrence of repunit primes and probable primes, it is conjectured strongly that there are infinitely many unique primes. (Any repunit prime is unique.)

As of 2010 the repunit (10²⁷⁰³⁴³-1)/9 is the largest known probable unique prime.^[1]

In 1996 the largest proven unique prime was (10¹¹³² + 1)/10001 or, using the notation above, (99990000)₁₄₁+ 1. Its reciprocal period is 2264. The record has been improved many times since then. As of 2010 the largest proven unique prime has 10,081 digits.^[2]

Base 2 Unique primes

3, 5, 7, 11, 13, 17, 19, 31, 41, 43, 73, 127, 151, 241, 257, 331, 337, 683, ...... (sequence A144755 in OEIS)：

The Period length of them are: 2, 4, 3, 10, 12, 8, 18, 5, 20, 14, 9, 7, 15, 24, 16, 30, 21, 22, ......(sequence A161508 in OEIS)：

References

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.