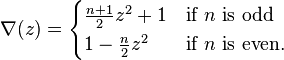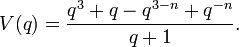Twist knot

From Wikipedia, the free encyclopedia

A twist knot with six half-twists.

In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together. (That is, a twist knot is any Whitehead double of an unknot.) The twist knots are an infinite family of knots, and are considered the simplest type of knots after the torus knots.

Construction

A twist knot is obtained by linking together the two ends of a twisted loop. Any number of half-twists may be introduced into the loop before linking, resulting in an infinite family of possibilities. The following figures show the first few twist knots:

One half-twist
(trefoil knot)
Two half-twists
(figure-eight knot)
Three half-twists
(5₂ knot)
Four half-twists
(stevedore knot)
Five half-twists
(7₂ knot)
Six half-twists
(8₁ knot)

Properties

The four half-twist stevedore knot is created by passing the one end of an unknot with four half-twists through the other.

All twist knots have unknotting number one, since the knot can be untied by unlinking the two ends. Every twist knot is also a 2-bridge knot.^[1] Of the twist knots, only the unknot and the stevedore knot are slice knots.^[2] A twist knot with $n$ half-twists has crossing number $n+2$ . All twist knots are invertible, but the only amphichiral twist knots are the unknot and the figure-eight knot.

Invariants

The invariants of a twist knot depend on the number $n$ of half-twists. The Alexander polynomial of a twist knot is given by the formula

$\Delta (t)={\begin{cases}{\frac {n+1}{2}}t-n+{\frac {n+1}{2}}t^{{-1}}&{\text{if }}n{\text{ is odd}}\\-{\frac {n}{2}}t+(n+1)-{\frac {n}{2}}t^{{-1}}&{\text{if }}n{\text{ is even,}}\\\end{cases}}$

and the Conway polynomial is

$\nabla (z)={\begin{cases}{\frac {n+1}{2}}z^{2}+1&{\text{if }}n{\text{ is odd}}\\1-{\frac {n}{2}}z^{2}&{\text{if }}n{\text{ is even.}}\\\end{cases}}$

When $n$ is odd, the Jones polynomial is

$V(q)={\frac {1+q^{{-2}}+q^{{-n}}-q^{{-n-3}}}{q+1}},$

and when $n$ is even, it is

$V(q)={\frac {q^{3}+q-q^{{3-n}}+q^{{-n}}}{q+1}}.$

References

↑ Rolfsen, Dale (2003). Knots and links. Providence, R.I: AMS Chelsea Pub. p. 114. ISBN 0-8218-3436-3.
↑ Weisstein, Eric W., "Twist Knot", MathWorld.

v t e Knot theory (knots and links)

Hyperbolic	Figure-eight (4₁) Three-twist (5₂) Stevedore (6₁) 6₂ 6₃ Endless (7₄) Perko pair (10₁₆₁) (−2,3,7) pretzel (12n242) Borromean rings (63 2)

Satellite	Composite knots Granny Square

Torus	Unknot (0₁) Trefoil (3₁) Cinquefoil (5₁) Septafoil (7₁) Carrick mat (8₁₈) Unlink (02 1) Hopf (22 1) Solomon's (42 1) Whitehead (52 1) L10a140

Invariants	Alternating Arf invariant Bridge no. 2-bridge Brunnian Chirality Invertible Crosscap no. Crossing no. Finite type invariant Hyperbolic volume Genus Knot group Link group Linking no. Polynomial Alexander Bracket HOMFLY Jones Kauffman Pretzel Prime list Stick no. Tricolorability Unknotting no.

Notation & operations	Alexander–Briggs notation Conway notation Dowker notation Mutation Reidemeister move Skein relation

Other	Berge Braid theory Complement Double torus Fibered Framed Knot List of knots and links Ribbon Slice Sum Twist Wild

Category Commons

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.