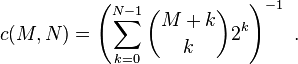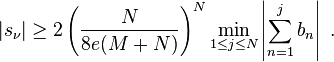Turán's method
In mathematics, Turán's method provides lower bounds for exponential sums and complex power sums. The method has been applied to problems in equidistribution.
The method applies to sums of the form
where the b and z are complex numbers and ν runs over a range of integers. There are two main results, depending on the size of the complex numbers z.
Turán's first theorem
The first result applies to sums sν where  for all n. For any range of ν of length N, say ν = M + 1, ..., M + N, there is some ν with |sν| at least c(M, N)|s0| where
for all n. For any range of ν of length N, say ν = M + 1, ..., M + N, there is some ν with |sν| at least c(M, N)|s0| where
The sum here may be replaced by the weaker but simpler 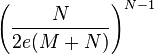 .
.
We may deduce Fabry's gap theorem from this result.
Turán's second theorem
The second result applies to sums sν where 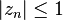 for all n. Assume that the z are ordered in decreasing absolute value and scaled so that |z1| = 1. Then there is some ν with
for all n. Assume that the z are ordered in decreasing absolute value and scaled so that |z1| = 1. Then there is some ν with
See also
- Turán's theorem in graph theory
References
- Montgomery, Hugh L. (1994). Ten lectures on the interface between analytic number theory and harmonic analysis. Regional Conference Series in Mathematics 84. Providence, RI: American Mathematical Society. ISBN 0-8218-0737-4. Zbl 0814.11001.