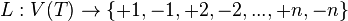Tucker's lemma

In the this example, where n=2, the red 1-simplex has vertices which are labelled by the same number with opposite signs. Tucker's lemma states that for such a triangulation at least one such 1-simplex must exist.

In mathematics, Tucker's lemma is a combinatorial analog of the Borsuk–Ulam theorem, named after Albert W. Tucker.

Let T be a triangulation of the closed n-dimensional ball Bⁿ. Assume T is antipodally symmetric on the boundary sphere S^n-1. That means that the subset of simplices of T which are in S^n-1 provides a triangulation of S^n-1 where if σ is a simplex then so is −σ. Let

be a labelling of the vertices of T which satisfies L(−v)=−L(v) for all vertices v in S^n-1. Then Tucker's lemma states that there exists a 1-simplex in T whose vertices are labelled by the same number but with opposite signs.

See also

• Brouwer fixed point theorem
• Sperner's lemma
• Topological combinatorics

References

• Freund, Robert M.; Todd, Michael J. (1981), "A constructive proof of Tucker's combinatorial lemma", Journal of Combinatorial Theory, Series A 30 (3): 321–325, doi:10.1016/0097-3165(81)90027-3, MR 618536 .
• Matoušek, Jiří (2003), Using the Borsuk–Ulam Theorem, Springer-Verlag, p. 34, ISBN 3-540-00362-2 .
• Tucker, A. W. (1946), "Some topological properties of disk and sphere", Proc. First Canadian Math. Congress, Montreal, 1945, Toronto: University of Toronto Press, pp. 285–309, MR 0020254 .