Truth-table reduction

From Wikipedia, the free encyclopedia

In computability theory, a truth-table reduction is a reduction from one set of natural numbers to another. As a "tool", it is weaker than Turing reduction, since not every Turing reduction between sets can be performed by a truth-table reduction, but every truth-table reduction can be performed by a Turing reduction. For the same reason it is said to be a stronger reducibility than Turing reducibility, because it implies Turing reducibility. A weak truth-table reduction is a related type of reduction which is so named because it weakens the constraints placed on a truth-table reduction, and provides a weaker equivalence classification; as such, a "weak truth-table reduction" can actually be more powerful than a truth-table reduction as a "tool", and perform a reduction which is not performable by truth table.

A Turing reduction from a set B to a set A computes the membership of a single element in A by asking questions about the membership of various elements in B during the computation; it may adaptively determine which questions it asks based upon answers to previous questions. In contrast, a truth-table reduction or a weak truth-table reduction must present all of its (finitely many) oracle queries at the same time. In a truth-table reduction, the reduction also gives a boolean function (a truth table) which, when given the answers to the queries, will produce the final answer of the reduction. In a weak truth-table reduction, the reduction uses the oracle answers as a basis for further computation which may depend on the given answers but may not ask further questions of the oracle.

Equivalently, a weak truth-table reduction is a Turing reduction for which the use of the reduction is bounded by a computable function. For this reason, they are sometimes referred to as bounded Turing (bT) reductions rather than as weak truth-table (wtt) reductions.

Properties

As every truth-table reduction is a Turing reduction, if A is truth-table reducible to B (A ≤_tt B), then A is also Turing reducible to B (A ≤_T B). Considering also one-one reducibility, many-one reducibility and weak truth-table reducibility, one gets the following chain of implications:

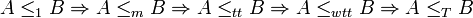$A\leq _{1}B\Rightarrow A\leq _{m}B\Rightarrow A\leq _{{tt}}B\Rightarrow A\leq _{{wtt}}B\Rightarrow A\leq _{T}B$ ; one-one reducibility implies many-one reducibility, which implies truth-table reducibility, which in turn implies weak truth-table reducibility, which in turn implies Turing reducibility.

References

H. Rogers, Jr., 1967. The Theory of Recursive Functions and Effective Computability, second edition 1987, MIT Press. ISBN 0-262-68052-1 (paperback), ISBN 0-07-053522-1

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.