Truncated 120-cell
 120-cell |
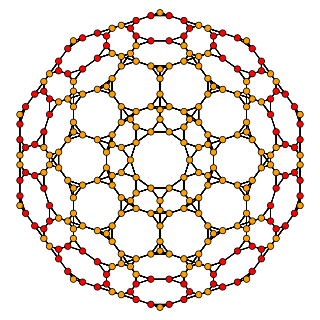 Truncated 120-cell |
 Rectified 120-cell |
 Bitruncated 120-cell |
 600-cell |
 Truncated 600-cell |
 Rectified 600-cell | |
| Orthogonal projections in H3 Coxeter plane | |||
|---|---|---|---|
In geometry, a truncated 120-cell is a uniform polychoron (4-dimensional uniform polytope) formed as the truncation of the regular 120-cell.
There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 600-cell.
Truncated 120-cell
| Truncated 120-cell | |
|---|---|
 Schlegel diagram (tetrahedron cells visible) | |
| Type | Uniform polychoron |
| Uniform index | 36 |
| Schläfli symbol | t0,1{5,3,3} |
| Coxeter-Dynkin diagrams | |
| Cells | 600 3.3.3 120 3.10.10 |
| Faces | 2400 triangles 720 decagons |
| Edges | 4800 |
| Vertices | 2400 |
| Vertex figure | 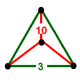 triangular pyramid |
| Dual | Tetrakis 600-cell |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The truncated 120-cell is a uniform polychoron, constructed by a uniform truncation of the regular 120-cell polychoron.
It is made of 120 truncated dodecahedral and 600 tetrahedral cells. It has 3120 faces: 2400 being triangles and 720 being decagons. There are 4800 edges of two types: 3600 shared by three truncated dodecahedra and 1200 are shared by two truncated dodecahedra and one tetrahedron. Each vertex has 3 truncated dodecahedra and one tetrahedron around it. Its vertex figure is an equilateral triangular pyramid.
Alternate names
- Truncated 120-cell (Norman W. Johnson)
- Tuncated hecatonicosachoron / Truncated polydodecahedron
- Truncated-icosahedral hexacosihecatonicosachoron (Acronym thi) (George Olshevsky, and Jonathan Bowers)[1]
Images
| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
 net |
 Central part of stereographic projection (centered on truncated dodecahedron) |
 Stereographic projection |
Bitruncated 120-cell
| Bitruncated 120-cell | ||
|---|---|---|
 Schlegel diagram, centered on truncated icosahedron, truncated tetrahedral cells visible | ||
| Type | Uniform polychoron | |
| Uniform index | 39 | |
| Coxeter-Dynkin diagram | ||
| Cells | 720: 120 5.6.6 600 3.6.6 | |
| Faces | 4320: 1200{3}+720{5}+ 2400{6} | |
| Edges | 7200 | |
| Vertices | 3600 | |
| Vertex figure | 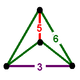 digonal disphenoid | |
| Schläfli symbol | t1,2{5,3,3} | |
| Symmetry group | H4, [3,3,5], order 14400 | |
| Properties | convex, vertex-transitive | |
The bitruncated 120-cell is a uniform polychoron. It has 720 cells: 120 truncated icosahedra, and 600 truncated tetrahedra. Its vertex figure is a digonal disphenoid, with two truncated icosahedra and two truncated tetrahedra around it.
Alternate names
- Bitruncated 120-cell / Bitruncated 600-cell (Norman W. Johnson)
- Bitruncated hecatonicosachoron / Bitruncated hexacosichoron / Bitruncated polydodecahedron / Bitruncated polytetrahedron
- Truncated-icosahedral hexacosihecatonicosachoron (Acronym Xhi) (George Olshevsky, and Jonathan Bowers)[2]
Images
 Stereographic projection (Close up) |
| H3 | A2 / B3 / D4 | A3 / B2 / D3 |
|---|---|---|
 [10] |
 [6] |
 [4] |
Truncated 600-cell
| Truncated 600-cell | |
|---|---|
 Schlegel diagram (icosahedral cells visible) | |
| Type | Uniform polychoron |
| Uniform index | 41 |
| Schläfli symbol | t0,1{3,3,5} |
| Coxeter-Dynkin diagram | |
| Cells | 720: 120 600 |
| Faces | 2400{3}+1200{6} |
| Edges | 4320 |
| Vertices | 1440 |
| Vertex figure |  pentagonal pyramid |
| Dual | Dodecakis 120-cell |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The truncated 600-cell is a uniform polychoron. It is derived from the 600-cell by truncation. It has 720 cells: 120 icosahedra and 600 truncated tetrahedra. Its vertex figure is a pentagonal pyramid, with one icosahedron on the base, and 5 truncated tetrahedra around the sides.
Alternate names
- Truncated 600-cell (Norman W. Johnson)
- Truncated hexacosichoron (Acronym tex) (George Olshevsky, and Jonathan Bowers)[3]
- Truncated tetraplex (Conway)
Structure
The truncated 600-cell consists of 600 truncated tetrahedra and 120 icosahedra. The truncated tetrahedral cells are joined to each other via their hexagonal faces, and to the icosahedral cells via their triangular faces. Each icosahedron is surrounded by 20 truncated tetrahedra.
Images
 Centered on icosahedron |
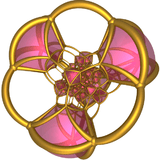 Centered on truncated tetrahedron |
 Central part and some of 120 red icosahedra. |
 Net |
| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
| 3D Parallel projection | |
|---|---|
 |
Parallel projection into 3 dimensions, centered on an icosahedron. Nearest icosahedron to the 4D viewpoint rendered in red, remaining icosahedra in yellow. Truncated tetrahedra in transparent green. |
Related polytopes
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
runcinated 120-cell |
bitruncated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell |
|---|---|---|---|---|---|---|---|---|
| {5,3,3} | t1{5,3,3} | t0,1{5,3,3} | t0,2{5,3,3} | t0,3{5,3,3} | t1,2{5,3,3} | t0,1,2{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} |
 |
 |
 |
 |
 |
 |
 |
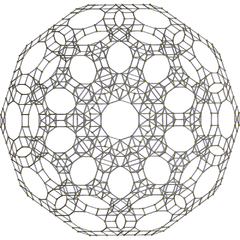 |
 |
 |
 |
 |
 |
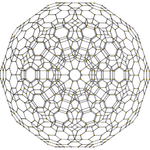 |
 | |||
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
runcinated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell |
| {3,3,5} | t1{3,3,5} | t0,1{3,3,5} | t0,2{3,3,5} | t0,3{3,3,5} | t1,2{3,3,5} | t0,1,2{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} |
Notes
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation m58 m59 m53
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 36, 39, 41, George Olshevsky.
- Richard Klitzing, 4D, uniform polytopes (polychora) o3o3x5x - thi, o3x3x5o - xhi, x3x3o5o - tex
- Four-Dimensional Polytope Projection Barn Raisings (A Zometool construction of the truncated 120-cell), George W. Hart
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | BCn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes | ||||||||||||