True airspeed

From Wikipedia, the free encyclopedia

A mechanical true airspeed indicator for an airplane. The pilot sets the altitude and air temperature in the top window using the knob; the needle indicates true airspeed in the lower left window.

The true airspeed (TAS; also KTAS, for knots true airspeed) of an aircraft is the speed of the aircraft relative to the airmass in which it is flying. The true airspeed is important information for accurate navigation of an aircraft.

Performance

TAS is the true measure of aircraft performance in cruise, thus listed in aircraft specs, manuals, performance comparisons, pilot reports, and every situation when actual performance needs to be measured. It is the speed normally listed on the flight plan, also used in flight planning, before considering the effects of wind.

Airspeed sensing errors

The airspeed indicator (ASI), driven by a Pitot tube and a barometric static port, shows what is called indicated airspeed (IAS). By the static port the IAS is corrected for the surrounding air pressure, but not for air density. The ratio between pressure and density is temperature dependent — as per the ideal gas law.

At sea level in the International Standard Atmosphere (ISA) and at low speeds where air compressibility is negligible, IAS corresponds to TAS. When the air density or temperature around the aircraft differs from standard sea level conditions, IAS will no longer correspond to TAS, thus it will no longer reflect aircraft performance. The ASI will indicate less than TAS when the air density decreases due to a change in altitude or air temperature.

For this reason, TAS cannot be measured directly. In flight, it can be calculated either by using an E6B flight calculator or its equivalent. For low speeds, the data required are static air temperature, pressure altitude and IAS (or CAS for more precision). Above approximately 100 knots, the compressibility error rises significantly and TAS must be calculated by the Mach speed. Mach incorporates the above data including the compressibility factor. Modern aircraft instrumentation use an Air Data Computer to perform this calculation in real time and display the TAS reading directly on the EFIS.

Since temperature variations are of a smaller influence, the ASI error can be roughly estimated as indicating about 2% less than TAS per 1,000ft of altitude above sea level. For example, an aircraft flying at 15,000ft in the international standard atmosphere with an IAS of 100kt, is actually flying at 126kt TAS.

Use in navigation calculations

To maintain a desired ground track whilst flying in the moving airmass, the pilot of an aircraft must use knowledge of wind speed, wind direction, and true air speed to determine the required heading. See also wind triangle.

Calculating true airspeed

Low-speed flight

At low speeds and altitudes, IAS and CAS are close to equivalent airspeed (EAS). TAS can be calculated as a function of EAS and air density:^[1]

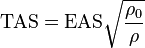
${\mathrm {TAS}}={\mathrm {EAS}}{\sqrt {{\frac {\rho _{0}}{\rho }}}}$

where

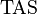${\mathrm {TAS}}$ is true airspeed

${\mathrm {EAS}}$ is equivalent airspeed

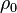$\rho _{0}$ is the air density at sea level in the International Standard Atmosphere (15°C and 1013.25 hectopascals) (density of 1.225 kg/m³)

$\rho$ is the density of the air in which the aircraft is flying

High-speed flight

TAS can be calculated as a function of Mach number and static air temperature:

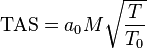
${\mathrm {TAS}}={a_{0}}M{\sqrt {T \over T_{0}}}$

Where: ${a_{0}}$ is the speed of sound at standard sea level (661.47 knots); $M$ is Mach number,; $T$ is static air temperature in kelvin,; $T_{0}$ is the temperature at standard sea level (288.15 K)

For manual calculation of TAS in knots where Mach number and static air temperature are known, the expression may be simplified to:

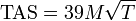
${\mathrm {TAS}}=39M{\sqrt {T}}$

(remembering temperature is in kelvin)

Combining the above with the expression for Mach number gives an expression for TAS as a function of impact pressure, static pressure and static air temperature (valid for subsonic flow):

${\mathrm {TAS}}={a_{0}}{\sqrt {{5T \over T_{0}}\left[\left({\frac {q_{c}}{P}}+1\right)^{{\frac {2}{7}}}-1\right]}}$

Where: ${q_{c}}$ is impact pressure; $P$ is static pressure

Electronic Flight Instrument Systems (EFIS) contain an air data computer with inputs of impact pressure, static pressure and total air temperature. In order to compute TAS the air data computer must convert total air temperature to static air temperature. This is also a function of Mach number:

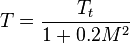
$T={{\frac {T_{{t}}}{1+0.2M^{2}}}}$

Where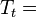: $T_{{t}}=$ total air temperature

In simple aircraft, without an air data computer or Machmeter, true airspeed can be calculated as a function of calibrated airspeed and local air density (or static air temperature and pressure altitude which determine density). Some airspeed indicators incorporate a slide rule mechanism to perform this calculation. Otherwise, it can be performed using this applet or a device such as the E6B (a handheld circular slide rule).

Notes

↑ Clancy, L.J., Aerodynamics, Section 3.8

References

Air Navigation. Department of the Air Force. 1 December 1989. AFM 51-40.
Clancy, L.J.(1975), Aerodynamics, Chapter 3. Pitman Publishing Limited, London. ISBN 0-273-01120-0
Kermode, A.C., Mechanics of Flight, Chapter 2. (Eighth edition 1972) Pitman Publishing Limited, London. ISBN 0-273-31623-0

External links

A free windows calculator which converts between various airspeeds (true / equivalent / calibrated) according to the appropriate atmospheric (standard and not standard!) conditions
True, Equivalent, and Calibrated Airspeed at MathPages
Newbyte airspeed converter, Android Version
avc.obsment.com - True airspeed calculator.
Calculate True Airspeed, Mach, Pitot Tube Impact Air Pressure and more at luizmonteiro.com

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.