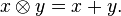Tropical geometry

From Wikipedia, the free encyclopedia
A tropical cubic curve

Tropical geometry is a relatively new area in mathematics, which might loosely be described as a piece-wise linear or skeletonized version of algebraic geometry. Its leading ideas had appeared in different guises in previous works of George M. Bergman and of Robert Bieri and John Groves, but only since the late nineties has an effort been made to consolidate the basic definitions of the theory. This effort has been in great part motivated by the strong applications to enumerative algebraic geometry uncovered by Grigory Mikhalkin.

The adjective tropical is given in honor of the Brazilian mathematician Imre Simon, who pioneered the field.

Basic definitions

We will use the min convention, that tropical addition is classical minimum. It is also possible to cast the whole subject in terms of the max convention, negating throughout, and several authors make this choice.

Consider the tropical semiring (also known as the min-plus algebra due to the definition of the semiring). This semiring, (ℝ ∪ {∞}, ⊕, ⊗), is defined with the operations as follows:

x\oplus y=\min\{\,x,y\,\},\,
x\otimes y=x+y.\,

From this we can also define tropical exponentiation in the usual way as iterated tropical products.

A monomial of variables in this semiring is a linear map, represented in classical arithmetic as a linear function of the variables with integer coefficients.[1] A polynomial in the semiring is the minimum of a finite number of such monomials, and is therefore a concave, continuous, piecewise linear function.

The set of points where a tropical polynomial F is non-differentiable is called its associated tropical hypersurface.

There are two important characterizations of these objects:

  1. Tropical hypersurfaces are exactly the rational polyhedral complexes satisfying a "zero-tension" condition.
  2. Tropical surfaces are exactly the non-Archimedean amoebas over an algebraically closed non-archimedean field K.[2]

These two characterizations provide a "dictionary" between combinatorics and algebra. Such a dictionary can be used to take an algebraic problem and solve its easier combinatorial counterpart instead.

The tropical hypersurface can be generalized to a tropical variety by taking the non-archimedean amoeba of ideals I in K[x1, ..., xn] instead of polynomials. It has been proved that the tropical variety of an ideal I equals the intersection of the tropical hypersurfaces associated to every polynomial in I. This intersection can be chosen to be finite.

There are a number of articles and surveys on tropical geometry. The study of tropical curves (tropical hypersurfaces in ℝ2) is particularly well developed. In fact, for this setting, mathematicians have established analogues of many classical theorems; e.g., Pappus's theorem, Bézout's theorem, the degree-genus formula, and the group law of the cubics[3] all have tropical counterparts.

See also

References

  1. ↑ David Speyer and Bernd Sturmfels. "Tropical Mathematics". Arxiv. Retrieved 30 January 2014. 
  2. ↑ Mikhalkin, Grigory (2004). "Amoebas of algebraic varieties and tropical geometry". In Donaldson, Simon; Eliashberg, Yakov; Gromov, Mikhael. Different faces of geometry. International Mathematical Series (New York) 3. New York, NY: Kluwer Academic/Plenum Publishers. pp. 257–300. ISBN 0-306-48657-1. Zbl 1072.14013. 
  3. ↑ Chan, Melody; Sturmfels, Bernd (2013). "Elliptic curves in honeycomb form". In Brugallé, Erwan. Algebraic and combinatorial aspects of tropical geometry. Proceedings based on the CIEM workshop on tropical geometry, International Centre for Mathematical Meetings (CIEM), Castro Urdiales, Spain, December 12–16, 2011. Contemporary Mathematics 589. Providence, RI: American Mathematical Society. pp. 87–107. ISBN 978-0-8218-9146-9. Zbl 06241528. 
  • Bogart, Tristram; Jensen, Anders; Speyer, David; Sturmfels, Bernd; Thomas, Rehka (2005). "Computing Tropical Varieties". arXiv:math/0507563v1 [math.AG].
  • Einsiedler, Manfred; Kapranov, Mikhail; Lind, Douglas (2005). "Non-archimedean amoebas and tropical varieties". arXiv:math/0408311v2 [math.AG].
  • Gathmann, Andreas (2006). "Tropical algebraic geometry". arXiv:math/0601322v1 [math.AG].
  • Gross, Mark (2010). Tropical geometry and mirror symmetry. Providence, R.I.: Published for the Conference Board of the Mathematical Sciences by the American Mathematical Society with support from the National Science Foundation. ISBN 9780821852323. 
  • Itenberg, Illia; Grigory Mikhalkin, Eugenii Shustin (2009). Tropical algebraic geometry (2nd ed.). Basel: Birkhäuser Basel. ISBN 9783034600484. 
  • Mikhalkin, Grigory (2006). "Tropical Geometry and its applications". arXiv:math/0601041v2 [math.AG].
  • Mikhalkin, Grigory (2004). "Enumerative tropical algebraic geometry in R2". arXiv:math/0312530v4 [math.AG].
  • Mikhalkin, Grigory (2004). "Amoebas of algebraic varieties and tropical geometry". arXiv:math/0403015v1 [math.AG].
  • Pachter, L.; Sturmfels, Bernd (2004). "Tropical geometry of statistical models". Proceedings of the National Academy of Sciences 101 (46): 16132–16137. doi:10.1073/pnas.0406010101. 
  • Speyer, David E. (2003). "The Tropical Grassmannian". arXiv:math/0304218v3 [math.AG].
  • Speyer, David; Sturmfels, Bernd (2004). "Tropical Mathematics". arXiv:math/0408099v1 [math.AG].
  • Theobald, Thorsten (2003). "First steps in tropical geometry". arXiv:math/0306366v2 [math.AG].

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.