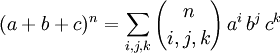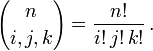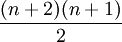Trinomial expansion

From Wikipedia, the free encyclopedia

In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials. The expansion is given by

(a+b+c)^{n}=\sum _{{i,j,k}}{n \choose i,j,k}\,a^{i}\,b^{j}\,c^{k}

where n is a nonnegative integer and the sum is taken over all combinations of nonnegative indices i, j, and k such that i + j + k = n. The trinomial coefficients are given by

{n \choose i,j,k}={\frac {n!}{i!\,j!\,k!}}\,.

This formula is a special case of the multinomial formula for m = 3. The coefficients can be defined with a generalization of Pascal's triangle to three dimensions, called Pascal's pyramid or Pascal's tetrahedron.

The number of terms of an expanded trinomial is

{\frac {(n+2)(n+1)}{2}}

where n is the exponent to which the trinomial is raised.

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.