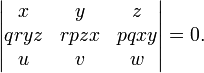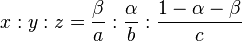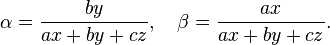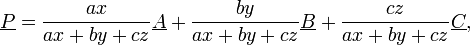Trilinear coordinates

From Wikipedia, the free encyclopedia

In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates. They are often called simply "trilinears".

Examples

The trilinears of the incenter of a triangle ABC is 1 : 1 : 1; that is, the (directed) distances from the incenter to the sidelines BC, CA, AB are proportional to the actual distances denoted by (r, r, r), where r is the inradius of triangle ABC.

Note that the symbol x:y:z(for trilinears) is different from (kx, ky, kz)(for actual directed distances),

where k can be determined by the formula: 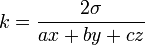$k={\frac {2\sigma }{ax+by+cz}}$ ,

where a, b, c are the respective sidelengths BC, CA, AB, and σ = area of ABC. ("Comma notation" for trilinears should be avoided, because the notation (x, y, z), which means an ordered triple, does not allow, for example, (x, y, z) = (2x, 2y, 2z), whereas the "colon notation" does allow x : y : z = 2x : 2y : 2z.)

A = 1 : 0 : 0
B = 0 : 1 : 0
C = 0 : 0 : 1
incenter = 1 : 1 : 1
centroid = bc : ca : ab = 1/a : 1/b : 1/c = csc A : csc B : csc C.
circumcenter = cos A : cos B : cos C.
orthocenter = sec A : sec B : sec C.
nine-point center = cos(B − C) : cos(C − A) : cos(A − B).
symmedian point = a : b : c = sin A : sin B : sin C.
A-excenter = −1 : 1 : 1
B-excenter = 1 : −1 : 1
C-excenter = 1 : 1 : −1.

Note that, in general, the incenter is not the same as the centroid; the centroid has barycentric coordinates 1 : 1 : 1 (these being proportional to actual signed areas of the triangles BGC, CGA, AGB, where G = centroid.)

Formulas

Trilinears enable many algebraic methods in triangle geometry. For example, three points

P = p : q : r

U = u : v : w

X = x : y : z

are collinear if and only if the determinant

$D={\begin{vmatrix}p&q&r\\u&v&w\\x&y&z\end{vmatrix}}$

equals zero. The dual of this proposition is that the lines

pα + qβ + rγ = 0

uα + vβ + wγ = 0,

xα + yβ + zγ = 0

concur in a point if and only if D = 0.

Also, if the actual directed distances are used when evaluating determinant D, then (area of (PUX)) = KD, where K = abc/8σ² if triangle PUX has the same orientation as triangle ABC, and K = - abc/8σ² otherwise.

Many cubic curves are easily represented using trilinears. For example, the pivotal self-isoconjugate cubic Z(U,P), as the locus of a point X such that the P-isoconjugate of X is on the line UX is given by the determinant equation

${\begin{vmatrix}x&y&z\\qryz&rpzx&pqxy\\u&v&w\end{vmatrix}}=0.$

Among named cubics Z(U,P) are the following:

Thomson cubic: Z(X(2),X(1)), where X(2) = centroid, X(1) = incenter

Feuerbach cubic: Z(X(5),X(1)), where X(5) = Feuerbach point

Darboux cubic: Z(X(20),X(1)), where X(20) = De Longchamps point

Neuberg cubic: Z(X(30),X(1)), where X(30) = Euler infinity point.

Conversions

A point with trilinears α : β : γ has barycentric coordinates aα : bβ : cγ where a, b, c are the sidelengths of the triangle. Conversely, a point with barycentrics α : β : γ has trilinears α/a : β/b : γ/c.

There are formulas for converting between trilinear coordinates and 2D Cartesian coordinates. Given a reference triangle ABC, express the position of the vertex B in terms of an ordered pair of Cartesian coordinates and represent this algebraically as a vector a, using vertex C as the origin. Similarly define the position vector of vertex A as b. Then any point P associated with the reference triangle ABC can be defined in a 2D Cartesian system as a vector P = αa + βb. If this point P has trilinear coordinates x : y : z then the conversion formulas are:

$x:y:z={\frac {\beta }{a}}:{\frac {\alpha }{b}}:{\frac {1-\alpha -\beta }{c}}$

and

$\alpha ={\frac {by}{ax+by+cz}},\quad \beta ={\frac {ax}{ax+by+cz}}.$

If an arbitrary origin is chosen where the Cartesian coordinates of the vertices are known and represented by the vectors A, B and C and if the point P has trilinear coordinates x : y : z, then the Cartesian coordinates of P are the weighted average of the Cartesian coordinates of these vertices using the barycentric coordinates ax, by and cz as the weights.

Hence

$\underline {P}={\frac {ax}{ax+by+cz}}\underline {A}+{\frac {by}{ax+by+cz}}\underline {B}+{\frac {cz}{ax+by+cz}}\underline {C},$

where |C − B| = a, |A − C| = b and |B − A| = c.

References

Weisstein, Eric W., "Trilinear Coordinates", MathWorld.

External links

Encyclopedia of Triangle Centers - ETC by Clark Kimberling; has trilinear coordinates (and barycentric) for more than 3200 triangle centers

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.