Trihexagonal tiling

From Wikipedia, the free encyclopedia
Trihexagonal tiling

TypeSemiregular tiling
Vertex configuration(3.6)2
Schläfli symbolr{6,3}
h2{6,3}
Wythoff symbol2 | 6 3
3 3 | 3
Coxeter diagram
=
Symmetryp6m, [6,3], (*632)
p3m1, [3[3]], (*333)
Rotation symmetryp6, [6,3]+, (632)
p3, [3[3]]+, (333)
Bowers acronymThat
DualRhombille tiling
PropertiesVertex-transitive Edge-transitive

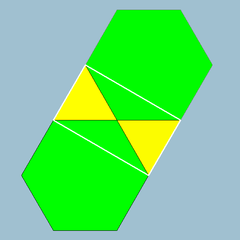Vertex figure: (3.6)2

In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex. It has Schläfli symbol of t1{6,3}; its edges form an infinite arrangement of lines.[1][2] It can also be constructed as a cantic hexagonal tiling, h2{6,3}, if drawn by alternating two colors of triangles.

In physics as well as in Japanese basketry, the same pattern is called a Kagome lattice. Conway calls it a hexadeltille, combining alternate elements from a hexagonal tiling (hextille) and triangular tiling (deltille).[3]

There are 3 regular and 8 semiregular tilings in the plane.

Kagome lattice

Japanese basket showing the kagome pattern

A kagome lattice originally referred to an arrangement of laths composed of interlaced triangles such that each point where two laths cross has four neighboring points, forming the pattern of a trihexagonal tiling. The name derives from the Japanese word kagome (籠目), a traditional woven bamboo pattern, composed from the words kago, meaning "basket", and me, literally meaning "eye(s)", referring to the pattern of holes in a woven basket. Although called a lattice, its crossing points do not form a mathematical lattice.

Some minerals, namely jarosites and herbertsmithite, contain layers with kagome lattice arrangement of atoms in their crystal structure. These minerals display novel physical properties connected with geometrically frustrated magnetism. The term is much in use nowadays in the scientific literature, especially by theorists studying the magnetic properties of a theoretical kagome lattice in two or three dimensions. The term "kagome lattice" in this context was coined by Japanese physicist Kōji Fushimi, who was working with Ichirō Shōji. The first paper[4] on the subject appeared in 1951.[5]

Uniform colorings

There are two distinct uniform colorings of a trihexagonal tiling. (Naming the colors by indices on the 4 faces around a vertex (3.6.3.6): 1212, 1232.)

Coloring
Wythoff symbol 2 | 6 3 3 3 | 3
Coxeter-Dynkin diagram =

Related polyhedra and tilings

A tiling with alternate large and small triangles is topologically identical to the trihexagonal tiling, but has a different symmetry group. The hexagons are distorted so 3 vertices are on the mid-edge of the larger triangles. As with the trihexagonal tiling, it has two uniform colorings:

The trihexagonal tiling is also one of eight uniform tilings that can be formed from the regular hexagonal tiling (or the dual triangular tiling) by a Wythoff construction. Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)

Uniform hexagonal/triangular tilings
Symmetry: [6,3], (*632) [6,3]+
(632)		 [1+,6,3]
(*333)		 [6,3+]
(3*3)
{6,3} t{6,3} r{6,3}
r{3[3]}		 t{3,6}
t{3[3]}		 {3,6}
{3[3]}		 rr{6,3}
s2{6,3}		 tr{6,3} sr{6,3} h{6,3}
{3[3]}		 h2{6,3}
r{3[3]}		 s{3,6}
s{3[3]}

=
=
= 		=
or 		=
or
=





Uniform duals
V63 V3.122 V(3.6)2 V63 V36 V3.4.12.4 V.4.6.12 V34.6 V36 V(3.6)2 V36
Triangle
symmetry		 Extended
symmetry		 Extended
diagram		 Extended
order		 Honeycomb diagrams
a1 [3[3]] ×1 (None)
i2 <[3[3]]>
= [6,3]
= 		×2 1, 2
r6 [3[3[3]]]
= [6,3]
= 		×6 3, (1)
Wythoff 3 | 3 3 3 3 | 3 3 | 3 3 3 3 | 3 3 | 3 3 3 3 | 3 3 3 3 | | 3 3 3
Coxeter
Image
Vertex figure
(3.3)3
3.6.3.6
(3.3)3
3.6.3.6
(3.3)3
3.6.3.6
6.6.6
3.3.3.3.3.3
Dimensional family of cantic polyhedra and tilings: 3.6.n.6
Symmetry
*n32
[1+,2n,3]
= [(n,3,3)]		 Spherical Planar Hyperbolic...
*332
[1+,4,3]
Td		 *333
[1+,6,3]
P3m1		 *433
[1+,8,3]...
 		 *∞33
[1+,∞,3]
 
Cantic
figure
3.6.2.6
3.6.3.6
3.6.4.6
3.6.∞.6
Coxeter
Schläfli
h2{4,3}
=
h2{6,3}
=
h2{8,3}
=
h2{∞,3}
=
Dual figure
V3.6.2.6
V3.6.3.6
V3.6.4.6
V3.6.∞.6
Coxeter

The trihexagonal tiling forms the case k = 6 in a sequence of quasiregular polyhedra and tilings, each of which has a vertex figure with two k-gons and two triangles:

Dimensional family of quasiregular polyhedra and tilings: 3.n.3.n
Symmetry
*n32
[n,3]		 Spherical Euclidean Hyperbolic tiling
*332
[3,3]
Td		 *432
[4,3]
Oh		 *532
[5,3]
Ih		 *632
[6,3]
p6m		 *732
[7,3]		 *832
[8,3]		 *∞32
[∞,3]
Quasiregular
figures
configuration
3.3.3.3
3.4.3.4
3.5.3.5
3.6.3.6
3.7.3.7
3.8.3.8
3.∞.3.∞
Coxeter diagram
Dual
(rhombic)
figures
configuration
V3.3.3.3
V3.4.3.4
V3.5.3.5
V3.6.3.6
V3.7.3.7
V3.8.3.8
V3.∞.3.∞
Coxeter diagram

The subset of this sequence in which k is an even number has (*n33) reflectional symmetry.

See also

Wikimedia Commons has media related to Uniform tiling 3-6-3-6.

References

  1. ↑ Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1.  (Chapter 2.1: Regular and uniform tilings, p.58-65)
  2. ↑ Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 38. ISBN 0-486-23729-X. 
  3. ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
  4. ↑ "I. Syôzi, Prog. Theor. Phys. 6, 306 (1951).". 
  5. ↑ "Physics Today article on the word kagome". 

External links

Wikimedia Commons has media related to Kagome structures.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.