Trigenus

From Wikipedia, the free encyclopedia

In low-dimensional topology, the trigenus of a closed 3-manifold is an invariant consisting of an ordered triple 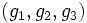$(g_{1},g_{2},g_{3})$ . It is obtained by minimizing the genera of three orientable handle bodies — with no intersection between their interiors— which decompose the manifold as far as the Heegaard genus need only two.

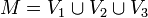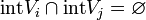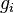That is, a decomposition $M=V_{1}\cup V_{2}\cup V_{3}$ with ${{\rm {int}}}V_{i}\cap {{\rm {int}}}V_{j}=\varnothing$ for $i,j=1,2,3$ and being $g_{i}$ the genus of $V_{i}$ .

For orientable spaces, 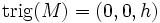${{\rm {trig}}}(M)=(0,0,h)$ , where $h$ is $M$ 's Heegaard genus.

For non-orientable spaces the ${{\rm {trig}}}$ has the form ${{\rm {trig}}}(M)=(0,g_{2},g_{3})\quad {\mbox{or}}\quad (1,g_{2},g_{3})$ depending on the image of the first Stiefel–Whitney characteristic class $w_{1}$ under a Bockstein homomorphism, respectively for $\beta (w_{1})=0\quad {\mbox{or}}\quad \neq 0.$

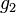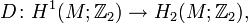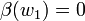It has been proved that the number $g_{2}$ has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface $G$ which is embedded in $M$ , has minimal genus and represents the first Stiefel–Whitney class under the duality map $D\colon H^{1}(M;{{\mathbb {Z}}}_{2})\to H_{2}(M;{{\mathbb {Z}}}_{2}),$ , that is, $Dw_{1}(M)=[G]$ . If $\beta (w_{1})=0\,$ then ${{\rm {trig}}}(M)=(0,2g,g_{3})\,$ , and if $\beta (w_{1})\neq 0.\,$ then ${{\rm {trig}}}(M)=(1,2g-1,g_{3})\,$ .

Theorem

A manifold S is a Stiefel–Whitney surface in M, if and only if S and M−int(N(S)) are orientable .

References

J.C. Gómez Larrañaga, W. Heil, V.M. Núñez. Stiefel–Whitney surfaces and decompositions of 3-manifolds into handlebodies, Topology Appl. 60 (1994), 267–280.
J.C. Gómez Larrañaga, W. Heil, V.M. Núñez. Stiefel–Whitney surfaces and the trigenus of non-orientable 3-manifolds, Manuscripta Math. 100 (1999), 405–422.
"On the trigenus of surface bundles over $S^{1}$ ", 2005, Soc. Mat. Mex. | pdf

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.