Triclinic crystal system

From Wikipedia, the free encyclopedia
An example of the triclinic crystals, microcline
Triclinic (a ≠ b ≠ c and α ≠ β ≠ γ )

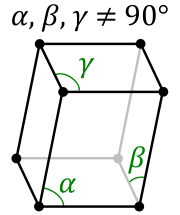
In crystallography, the triclinic crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. In addition, none of the three vectors are orthogonal to another.

The triclinic lattice is the least symmetric of the 14 three-dimensional Bravais lattices. It has (itself) the minimum symmetry all lattices have: points of inversion at each lattice point and at 7 more points for each lattice point: at the midpoints of the edges and the faces, and at the center points. It is the only lattice type that itself has no mirror planes.

Crystal classes

The triclinic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,[1] orbifold, type, and space groups are listed in the table below. There are a total 2 space groups.

# Point group Example Type Space group
Class Schönflies Intl orbifold Coxeter
1 Pedial [2] C1111[ ]+ Tantite enantiomorphic polar P1
2 Pinacoidal [2] Ci (= S2) 11×[2+,2+] Wollastonite centrosymmetric P1

With each only one space group is associated. Pinacoidal is also known as triclinic normal. Pedial is also triclinic hemihedral

Mineral examples include plagioclase, microcline, rhodonite, turquoise, wollastonite and amblygonite, all in triclinic normal (1).

See also

References

  1. ↑ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. 
  2. ↑ 2.0 2.1 "The 32 crystal classes". Retrieved 2009-07-08. 
  • Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., pp. 64 – 65, ISBN 0-471-80580-7
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.