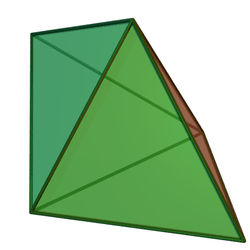
Triangular bipyramid

Triangular bipyramid
Type	Bipyramid and Johnson J11 - J12 - J13
Schläfli symbol	{ } + {3}
Coxeter diagram
Faces	6 triangles
Edges	9
Vertices	5
Face configuration	V3.4.4
Symmetry group	D3h, [3,2], (*223) order 12
Rotation group	D3, [3,2]+, (223), order 6
Dual	Triangular prism
Properties	Convex, face-transitive

In geometry, the triangular bipyramid (or dipyramid) is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.

It is also one of the Johnson solids, (J₁₂) with equilateral triangle faces. As the name suggests, it can be constructed by joining two tetrahedra along one face. It is a convex deltahedron. Although all its faces are congruent and the solid is face-transitive, it is not a Platonic solid because some vertices adjoin three faces and others adjoin four. As a Johnson solid, with 6 equilateral triangles, it is also in the set of deltahedra.

A Johnson solid is one of 92 strictly convex regular-faced polyhedra, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. They are named by Norman Johnson who first enumerated the set in 1966.

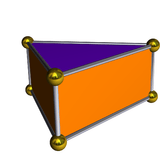
Dual polyhedron

The dual of the Johnson solid triangular bipyramid is the triangular prism, with 5 faces: 3 rectangular faces and 2 triangular.

Dual triangular bipyramid	Net of dual

Related polyhedra

The triangular bipyramid can be constructed by augmentation of smaller ones, specifically two stacked regular octahedra with 4 triangular bipyramids added around the sides, and 1 tetrahedron above and below. This polyhedron has 24 equilateral triangle faces, but it is not a Johnson solid because it has coplanar faces. It is a coplanar 24 triangle deltahedron. This polyhedron exists as the augmentation of cells in a gyrated alternated cubic honeycomb. Larger triangular polyhedra can be generated similarly, like 9, 16 or 25 triangles per larger triangle face, seen as a section of a triangular tiling.

See also

• Trigonal bipyramidal molecular geometry

Family of bipyramids

2	3	4	5	6	7	8	9	10	11	12	...	∞
As spherical polyhedra

External links

• Weisstein, Eric W., "Dipyramid", MathWorld.
  • Weisstein, Eric W., "Triangular dipyramid", MathWorld.