Triangular cupola

From Wikipedia, the free encyclopedia

Triangular cupola

Type	Johnson J₂ - J₃ - J₄
Faces	1+3 triangles 3 squares 1 hexagon
Edges	15
Vertices	9
Vertex configuration	6(3.4.6) 3(3.4.3.4)
Symmetry group	C_3v
Dual polyhedron	-
Properties	convex
Net

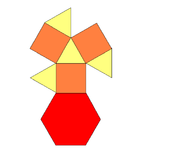In geometry, the triangular cupola is one of the Johnson solids (J₃). It can be seen as half a cuboctahedron.

A Johnson solid is one of 92 strictly convex regular-faced polyhedra, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. They are named by Norman Johnson who first enumerated the set in 1966.

Formulae

The following formulae for the volume and surface area can be used if all faces are regular, with edge length a:^[1]

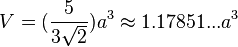
$V=({\frac {5}{3{\sqrt {2}}}})a^{3}\approx 1.17851...a^{3}$

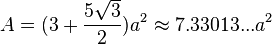
$A=(3+{\frac {5{\sqrt {3}}}{2}})a^{2}\approx 7.33013...a^{2}$

Dual polyhedron

The dual of the triangular cupola has 12 triangular faces:

Dual triangular cupola	Net of dual

Related polyhedra

The triangular cupola can be augmented by 3 square pyramids, leaving adjacent coplanar faces. This isn't a Johnson solid because of its coplanar faces. Merging those coplanar triangles into larger ones, topologically this is another triangular cupola with isosceles trapezoidal side faces. If all the triangle are retained and the base hexagon is replaced by 6 triangles, it generates a coplanar deltahedron with 22 faces.

The family of cupolae with regular polygons exists up to 5-sides, and higher for isosceles triangle version.

Family of cupolae
2	3	4	5	6
Digonal cupola	Triangular cupola	Square cupola	Pentagonal cupola	Hexagonal cupola (Flat)

References

↑ Stephen Wolfram, "Triangular cupola" from Wolfram Alpha. Retrieved July 20, 2010.

External links

Eric W. Weisstein, Triangular cupola (Johnson solid) at MathWorld

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.